Lorsque l'on fait du filtrage analogique, on peut être tenter, pour diverses raisons, de mettre bout à bout des filtres passifs d'ordre faible afin de réaliser un filtre d'ordre plus élevé de manière simple et rapide.
Ceci pourrait sembler une solution efficace pour réaliser des tests avec peu de composants. Néanmoins, la mise en séries de plusieurs étages passifs demande certaines précautions si l'on ne veux pas obtenir au final un filtre qui ne correspond pas du tout à ce que l'on a prévu d'avoir.
Cet article se basera sur la conception d'un filtre passe-bande passif en mettant en série un passe-bas passif du premier ordre avec un passe-haut passif du premier ordre. Nous verrons donc les problèmes liés aux impédances de ces deux montages, nous essayerons de calculer la fonction de transfert de ce filtre qui peut parraitre simple à première vue, puis je conclurais sur les précautions à prendre lorsque l'on connecte deux étages entre eux.
Montages en séries et impédances
En électronique, on prend souvent bien garde à calculer les impédances d'entrée et de sortie des différents étages du montages. Dans la majorité des cas, on essaye d'avoir une très forte impédance d'entrée et une très faible impédance de sortie. Ainsi, on est sûr que les montages branchés en entrée et en sortie du notre, n'influenceront pas son comportement.
Si on prend l'exemple simple d'un bloc d'alimentation. Cette alimentation possède une résistance interne appelé résistance du générateur. Si cette résistance est petite, alors on peut sans problème brancher des charges importantes en sortie sans que cela influe sur la tension de sortie.
A l'inverse, si la résistance interne du générateur devient non négligeable par rapport à la charge de sortie, alors la résistance du générateur et la charge forment un pont diviseur qui influe donc sur la tension de sortie !
C'est exactement le même problème avec la mise en série d'un passe-bas passif et d'un passe-haut passif : les impédances d'entrée et de sortie de mes deux filtres sont du même ordre de grandeur. Ainsi, si on met un passe-haut et un passe-bas passif tout simple en série, les deux étages vont s'influencer mutuellement et les calculs qui se trouvaient être très simple pour les étages pris séparément deviennent beaucoup plus compliqués !
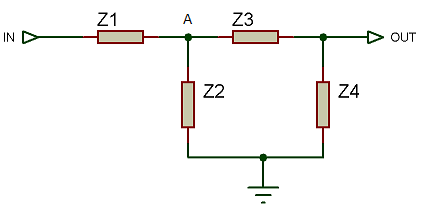
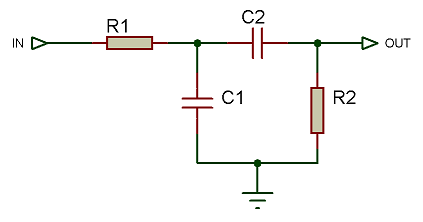
Filtre en double L
Sans plus attendre, voici la structure d'un filtre en double L :
Chacun des quatre composants est représenté ici par une impédance 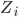 .
.
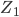 et
et 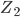 forment le première étage alors que
forment le première étage alors que 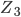 et
et 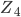 forment le second.
forment le second.
Nous pouvons donc commencer à essayer de calculer la fonction de transfert de manière générique, sans placer, pour le moment, les résistances et les condensateurs. Nous souhaitons exprimer la sortie en fonction de l'entrée. Pour cela, nous commençons à appliquer le théorème de Millman au point A.
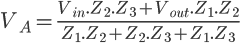
Maintenant, appliquons Millman à la sortie.
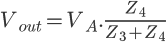
Il ne reste plus qu'a remplacer 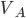 dans cette dernière équation et de triturer un peu l''ensemble pour obtenir la fonction de transfert générale d'un filtre en double L :
dans cette dernière équation et de triturer un peu l''ensemble pour obtenir la fonction de transfert générale d'un filtre en double L :
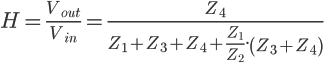
Passe-bande en double L
Maintenant que nous avons dégrossi le terrain, il est maintenant possible remplacer les impédances génériques par les composants. J'ai donc choisi de prendre l'exemple du passe-bande RC+CR
Attention à l'ordre des composants ! Le filtre RC+CR n'est pas le même que le CR+RC ! L'ordre des étages est ici important !
Ce que je cherche à obtenir, c'est une formule ayant une forme qui se rapproche de celle-ci :
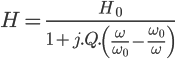
En effet, cette formulation est celle de la fonction de transfert générale d'un filtre passe-bande classique. A partir de cette forme, il est facile de calculer les fréquences de coupures.
Avant de remplacer les impédances, je vais remaniement un peu la fonction de transfert afin d'obtenir plus facilement la forme voulu par la suite :
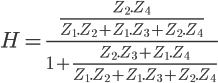
Maintenant, on remplace 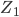 par
par 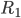 ,
, 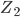 par
par 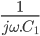 ,
, 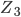 par
par 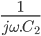 et
et 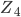 par
par 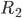 , ce qui nous donne :
, ce qui nous donne :
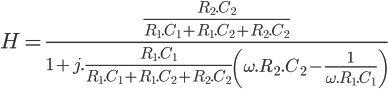
On a donc ici une formule qui commence à ressembler à ce que l'on souhaite ! On va maintenant fixer certaines valeurs des composants afin que la formule colle parfaitement au modèle. Pour cela, il faut que 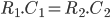 . On peut donc prendre
. On peut donc prendre 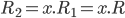 et
et 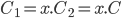 . Ce qui nous donne :
. Ce qui nous donne :
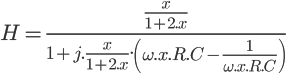
On a donc réussi à mettre la formule sous la forme souhaitée avec 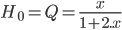 et
et 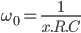
On peut donc maintenant calculer très simplement l’atténuation du filtre ainsi que ses fréquences de coupures :
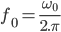
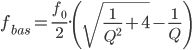
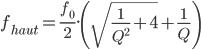
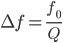
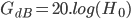
Conclusion
Lorsque l'on conçoit un circuit, aussi simple soit-il, il faut toujours garder en tête cette histoire d'impédance d'entrée et de sortie des étages. Si l'impédance d'entrée d'un étage n'est pas considéré comme grande vis à vis de la sortie de l'étage précédent, il faut alors isoler les deux étages à l'aide par exemple d'un suiveur (à amplificateur opérationnel ou à transistor) afin de ne pas créer d'interdépendances et ainsi, simplifier les calculs.
Quand ce n'est pas possible d'isoler les deux étages en questions, et à défaut de pouvoir calculer la fonction de transfert générale, il faut poser des contraintes sur certaines valeurs des composants afin de simplifier les calculs !

Salut Ferdi, c'est Seb, je viens de tomber completement par hasard sur ton site ^^
Bravo, il est plus reussi que le miens ^^ http://sebastien-barbry.sup.fr/
Super boulot, je vais le parcourir et prendre note.
J'espere que ca se passe bien chez WeGuide ^^
Salut.svp dans le cas de plusieurs étages la fonction de transfert n'est pas égale au produit des fonctions de transfert de tout les étages?