Toujours dans le but d'illustrer le dossier sur le Logique Floue, cet article présente un second et dernier exemple de système flou : le régulateur proportionnel intégrale flou (PI flou).
Le système flou sera assez basique et pourra être grandement améliorer le but étant avant tout de comprendre comment mettre en place une régulation flou de type PI. En fin d'article, j'expliquerais comment étendre l'exemple à un régulateur plus complet de type PID. Par contre, je n'ai pas fait de simulations, je vous laisse le soin de tester ce régulateur et d'effectuer les réglages vous-même.
Si vous ne connaissez pas le principe des régulateurs PI ou PID pour asservir un système, je vous conseille de faire une petite recherche sur le web ou de lire cet article qui explique le fonctionnement d'un PID : Implémenter un PID sans faire de calculs !
I Principe d'un régulateur PI
Dans l'article Implémenter un PID sans faire de calculs, j'explique comment fonctionne un régulateur de type PI : en définissant la commande comme combinaison linéaire de l'erreur et de la somme des erreurs du système, on arrive à obtenir un asservissement avec une erreur statique finale nulle. La formulation d'un tel régulateur est commande = Kp * erreur + Ki * somme(erreurs). Cette formulation fait intervenir le proportionnel et l'intégrateur en parallèle (commande = erreur + intégrale de l'erreur). Une autre formulation du régulateur PI peut être trouvé écrivant : variation de la commande = intégrale de ( la dérivé de l'erreur + l'erreur).
Ainsi, la formule commande = Kp * erreur + Ki * somme(erreurs) se transforme en commande(k) = commande(k-1) + Kp * variation(erreur) + Ki * erreur
C'est cette seconde formulation que l'on utilisera pour concevoir notre système flou. Ainsi, on a :
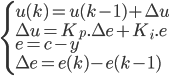
Avec :
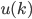 : la commande à l'instant k
: la commande à l'instant k : la variation de la commande
: la variation de la commande : l'erreur (e(k), l'erreur à l'instant k)
: l'erreur (e(k), l'erreur à l'instant k) : la variation de l'erreur (e(k) - e(k-1))
: la variation de l'erreur (e(k) - e(k-1)) : la consigne à respecter
: la consigne à respecter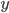 : la mesure de la réponse du système à la consigne donnée
: la mesure de la réponse du système à la consigne donnée
On voit bien que tout ce que l'on a à faire, c'est trouver la variation de la commande à appliquer à chaque instant en fonction de l'erreur et de sa variation. L'utilisation d'un système flou va nous permettre de ne pas nous soucier des coefficients Kp et Ki qui seront automatiquement déterminés en fonction des réglages que l'on aura fait sur notre système flou.
II Les variables linguistiques
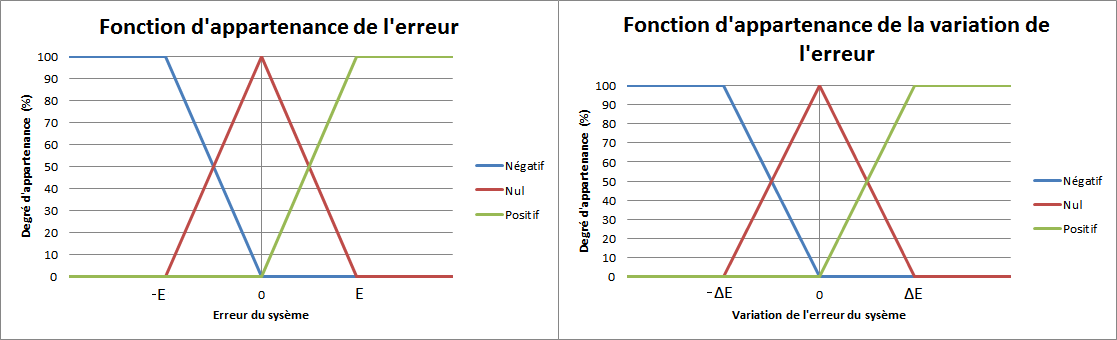
Les données que l'on a en entrées sont l'erreur et la variation de l'erreur. Chacune de ses entrées sera représentée par trois variables linguistiques. (erreur_négative, erreur_nulle, erreur_positive, variation_erreur_négative, variation_erreur_nulle et variation_erreur_positive).
Les fonctions d'appartenances sont de simples triangles ou fonctions linéaires :
Ici, on devra fixer 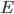 et
et 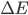 des fonctions d'appartenances par essais/erreurs en fonction du système.
des fonctions d'appartenances par essais/erreurs en fonction du système.
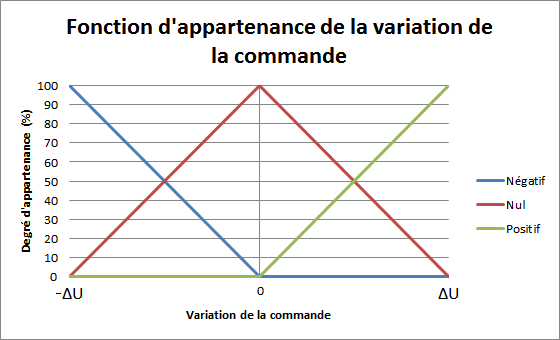
Enfin, pour la sortie, on choisira trois variables linguistiques représentant la variation de la commande (variation_commande_négative, variation_commande_nulle, variation_commande_positive). Les fonctions d’appartenances sont représentées ci-dessous :
De même que pour les fonctions d'appartenances des variables linguistiques d'entrée, 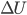 sera à déterminer expérimentalement.
sera à déterminer expérimentalement.
III Les règles d'inférences
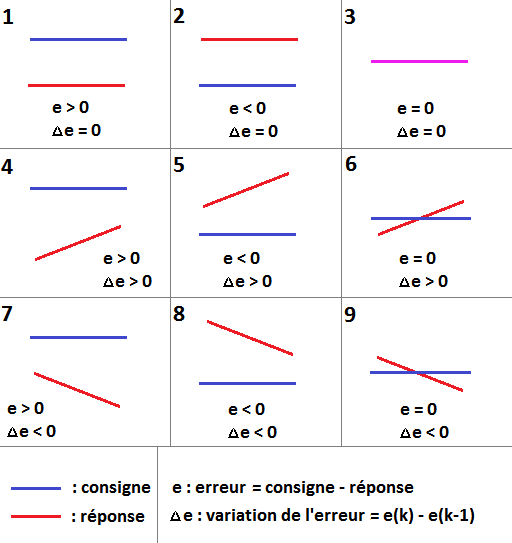
Il est temps maintenant de déterminer les divers règles à entrer au système. Comme il y a deux données d'entrées à trois variables linguistiques chacune, il y aura donc au maximum 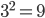 règles d'inférences. Ces neuf cas sont représentés schématiquement ci-dessous :
règles d'inférences. Ces neuf cas sont représentés schématiquement ci-dessous :
Cas un :
Dans ce premier cas, l'erreur est positive, ce qui veut dire que la réponse est inférieure à la consigne et la variation de l'erreur est nulle, ce qui veut dire que la réponse n'évolue pas. Dans ce cas, pour que la réponse atteigne la consigne, il faut augmenter la commande. La variation de la commande sera donc positive.
Cas deux :
A l'inverse, ici la réponse est supérieure à la consigne et n'évolue pas au cours du temps. Il faut donc diminuer la commande pour que la réponse atteigne la consigne. La variation de la commande est donc négative.
Cas trois :
Dans ce cas, la réponse n'évolue plus et vaut exactement la consigne. Dans ce cas-là, le système est asservit et il ne faut donc plus toucher à la commande. La variation de la commande est nulle.
Cas quatre :
Ici, la réponse est inférieure à la consigne, mais plus le temps passe et plus elle se rapproche de celle-ci. Il ne faut donc pas toucher à la commande. La variation de la commande sera nulle.
Cas cinq :
Dans ce cas-là par contre, la réponse est supérieure à la consigne (erreur négative) et elle continue à augmenter (donc à s'éloigner de la réponse). Ici, il faut diminuer fortement la commande. La variation de la commande sera donc négative.
Cas six :
L'erreur est nulle dans ce cas. Par contre, la réponse à tendance à vouloir dépasser la consigne. Il faut donc diminuer la commande. La variation de la commande est négative.
Cas sept :
Ici la réponse est bien en dessous de la consigne (erreur positive) et celle-ci diminue (variation de l'erreur négative). Il faut augmenter fortement la commande. La variation de la commande sera donc positive.
Cas huit :
Dans ce cas, la réponse est au-dessus de la consigne, mais elle tend à se rapprocher de celle-ci. Il ne faut donc pas toucher à la commande. La variation de la commande est nulle.
Cas neuf :
Enfin, dernier cas. La réponse est égal à la consigne, mais elle tend à diminuer. Pour contrer cela, il faut augmenter la commande. La variation de la commande sera positive.
Voilà. On a donc nos neuf règles prêtes à être utilisés !
- SI erreur positive ET variation_errreur nulle ALORS variation_commande positive
- SI erreur négative ET variation_errreur nulle ALORS variation_commande négative
- SI erreur nulle ET variation_errreur nulle ALORS variation_commande nulle
- SI erreur positive ET variation_errreur positive ALORS variation_commande nulle
- SI erreur négative ET variation_errreur positive ALORS variation_commande négative
- SI erreur nulle ET variation_errreur positive ALORS variation_commande négative
- SI erreur positive ET variation_errreur négative ALORS variation_commande positive
- SI erreur négative ET variation_errreur négative ALORS variation_commande nulle
- SI erreur nulle ET variation_errreur négative ALORS variation_commande positive
IV Réglage et amélioration du régulateur flou
Afin de tester ce système, vous devrez choisir les opérateurs logiques et la méthode de défuzzification à utiliser. Une fois ces paramètres fixés, vous pourrez chercher les valeurs de 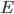 ,
, 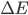 et
et 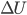 des fonctions d'appartenances afin de trouver le réglage qui correspond le mieux à votre cahier des charges.
des fonctions d'appartenances afin de trouver le réglage qui correspond le mieux à votre cahier des charges.
Afin d'améliorer ce régulateur, vous pouvez :
- Changer la forme des fonctions d'appartenances
- Rajouter des variables linguistiques en entrée
- Rajouter des variables linguistiques en sortie
- Rajouter ou modifier les règles d'inférences
V Le régulateur PID flou
Maintenant que l'on a vu le fonctionnement d'un régulateur de type PI, je vais toucher deux mots sur le régulateur PID. Dans l'article Implémenter un PID sans faire de calculs, on a vu qu'un PID classique s'écrivait 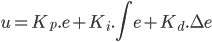 . Sur le même principe que pour le régulateur PI, on peut réécrire cette équation afin de mettre l'intégrateur en série plutôt qu'en parallèle. Ce qui nous donne
. Sur le même principe que pour le régulateur PI, on peut réécrire cette équation afin de mettre l'intégrateur en série plutôt qu'en parallèle. Ce qui nous donne 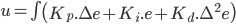 soit
soit 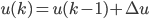 avec
avec 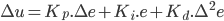 .
.
On se rend compte que le principe pour créer un PID flou est le même que pour le régulateur PI mis à part que l'on rajoute l'information dérivée seconde de l'erreur. Les variations de la variation de l'erreur seront ainsi à prendre en compte. Le nombre de règle à dresser sera donc plus importante.

Bonjour,
Je cherche a transformer mon régulateur flou à une équation simple comme : commande = K_erreur * erreur + K_derive_erreur * derive_erreue. pour diminue la puissance de calcule de µcontroleur à 8bit; sachent que la surface de lois sur Matlab est linéaire donc cette solution est possible par contre je ne vois pas comment faire autrement comment déterminer les deux gain (K_erreur et K_derive_erreur).
Cordialement,
Bonjour,
Si tu connais les caractéristiques précises de ton moteur, tu peux donc le modéliser mathématiquement et en déduire les coefficients qui permettront le meilleur compromis stabilité / rapidité.
Dans le cas général, il faut les déterminer à la main, par essais/erreurs.
As-tu lu ces articles ?
Le premier rappelle le principe d'un PID
Le second est un exemple d'implémentation du PID pour asservir en vitesse un moteur
je cherche comment appliquer un PI fou a une machine asynchrone ,je ss persdue,si vous pouvez m'aidez svp?
bonjour;
je suis un etudiant un peu agé donc je suis dépassé par la science informatique.mon sujet de these est l'optimisation de la culture de tomate sous serre.comme je suis agriculteur d'origine et je travaille.je sais les besons en température ,eau ..je cherche comment faire un régulateur pid flou selon Mamdani min_max les entrés sont ouverture de la vanne et la pression .sortie est l'humidité du sol qui doit etre située entre 40 et 80 %. l'agrégation dans l'intervalle donné.pour le régulateur comment trouvé l'erreur et sa dérivée?
merci de m'avoir aidé
Bonjour,
Sujet très intéressant et bien expliqué.
Serait-il possible d'avoir un résumé court sur le PD comme pour le PID.
Merci
Bonjour,
J'aurai besoin d'une précision complémentaire.
le terme (delta carré e) ne correspond certainement pas à (delta e au carré) mais faudrait-il l'interpréter comme un (delta e) sur 2 échantillonnages ?
Merci pour ton aide
Bonjour,
En effet, le terme (delta carré e) correspond à la dérivée seconde de l'erreur ; la variation de la variation de l'erreur.
Bonjour,
Merci pour la réponse.
Dans ce cas peut-on dire que :
delta carré de e = e(k) - 2e(k-1) + e(k-2)
Bonjour ,
En fait , je pense qu'après un raisonnement logique que la régle 4 est la régle numéro 7 et vice versa .
Car d'après la régle 4 , l'erreur est positif ce qui veut dire que la consigne est supérieur à la sortie .De plus, la variation de l'erreur est positif ce qui veut dire que l'erreur augmente, en d'autres termes, la sortie à tendance à s'éloigner de la consigne et puisque l'erreur est positif, ceci veut dire que la sortie va diminuer ,donc pour rétablir la situation, il faudra augmenter la consigne et par conséquent la variation de la commande sera positive .
Oui je suis d'accord avec vous !!
bonsoir ... alors la problématique que j'ai... c'est établir un controleur flou qui permet de noter les étudiants a la soutenance d'un projet de fin d'étude!!!!??? qu'est ce que je doit prendre comme variable linguistique et comment y remédier a ce problème???
bonjour comment je peut calculer l’erreur et leur variation
Bonjour
J’ai conçu un modèle de gestion d’énergie avec un régulateur en pi, le système ayant un supercondensateur avec un système de secours qui est une pile à combustible.
Le système marche avec la puissance du supercondensateur, une fois ce dernier se décharde, la pile prends le relais.
J’ai pris le même système et j’ai remplacé le régulateur pi par celui logique floue.
Mais la pile ne réagit pas.
Est-ce que le problème est dans le design du régulateur flou ?
Pour le régulateur pi j’ai comparé le soc (état de charge du supercondensateur) à une constante (entrée) et la sortie du pi comparé de nouveau à la puissance demandée, la sortie est la puissance de référence de la pile.
Pour le régulateur floue, on a 2 entrées (soc et puissance demandée) et la sortie est la puissance de référence de la pile.
Donc est ce que cette conception est bonne ?
Je ne peux pas changer les paramètres des sources car on changera uniquement les régulateurs pour un travail de comparaison entre les deux régulateurs.
A votre avis je dois régler quel paramètre ? Doit-on ajouter des paramètres dans le bloc du régulateur flou ?
Exemple : lors de la simulation : avec le régulateur pi à t=141,6 [S]
Puissance SC= 6031W. Puissance demandée= 6831,7W ; la pile réagit et délivre une puissance égale à 801,8 W.
Pour le même point (à t=141,6 [S]) j’ai relevé ceci avec le régulateur floue :
Puissance du SC=6030W et puissance demandée=6832,5W donc il faut une puissance de la pile = 6832,5 – 6030= 802,5W. Mais il indique une puissance de la pile très faible=0.00127W. Donc comment forcer le régulateur flou à ordonner à la pile de compenser cette différence ?
Cordialement
Bonjour !
" .... Cette formulation fait intervenir le proportionnel et l'intégrateur en parallèle (commande = erreur + intégrale de l'erreur)...."
comment vous êtes arrivé là ! ou sont passé le Kp et Ki ?
Recevez mes remerciements anticipés <3