La notion de filtre passe-bas, filtre passe-haut, coupe-bande ou passe-bande peut sembler familière aux électroniciens, en particulier si le signal à traiter est analogique. Un jeu de capacités, de résistances et éventuellement d'amplificateurs opérationnels suffit largement dans la majorité des cas. Le problème, c'est que tous ces beaux composants ne sont plus d'actualités lorsque l'on travaille avec des signaux numériques. A ce niveau, le concepteur d'un filtre numérique travaillera avec des microcontrôleurs ou des processeurs et manipulera un flux de nombre représentant le signal discrétisé.
Dans un monde utilisant de plus en plus le numérique, le filtrage numérique prend donc une place de plus en plus importante. On retrouve aujourd'hui des filtres numériques partout : dans les radios, les téléphones, les télévisions, les home cinémas, mais aussi en informatique, dans les logiciels de traitement audio, les lecteurs multimédias etc. Être capable de comprendre comment fonctionne de tels filtres est donc indispensable lorsque l'on touche au traitement du signal.
Nous allons donc voir dans cet article à quoi correspond concrètement les expressions mathématiques d'un filtre numérique (que l'on peut, par exemple, souvent trouver sur internet) et nous verrons comment implémenter de tels filtres dans un langage de programmation séquentiel. (Je vous fournirais ma bibliothèque codé en C)

I. Le filtre à réponse impulsionnelle finie (RIF)
Un signal continu peut être définie comme une somme de sinusoïdale. Le but d'un filtre est de jouer sur l'amplitude et la phase de ces sinusoïdes. Un filtre travaille donc dans le domaine fréquentiel et temporel. On peut donc comprendre que l'on filtre un signal en général et non une valeur du signal.
C'est la même chose lorsque l'on discrétise le signal : le filtre s'applique à l'ensemble du signal et non à l'échantillon en cours. Pour obtenir la valeur d'un échantillon après passage dans le filtre, on est donc obligé de considérer tous les échantillons du signal et d'appliquer des coefficients de pondération sur chacun des échantillons.
On peut donc définir un filtre numérique comme étant une somme pondéré de tous les échantillons du signal :
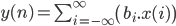
Avec y(n) l'échantillon numéro 'n' après filtrage, x(i), l'échantillon numéro 'i' du signal (avant filtrage) et 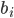 , le coefficient à appliquer à l'échantillon i.
, le coefficient à appliquer à l'échantillon i.
Bien évidemment, une telle équation est impossible à mettre en œuvre en réalité. En effet, on ne peut connaitre entièrement tout un signal. On ne le connait qu'à partir d'un certain moment jusqu'à un autre moment. C'est donc pour respecter le principe de causalité que l'on peut modifier cette formule :
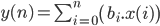
Dans ce cas, c'est déjà beaucoup mieux. Par contre, avec cette formule, on est obligé de garder en mémoire tout le signal, ce qui est des fois infaisables en pratique. De plus, les coefficients associés aux premiers échantillons deviendront de plus en plus faible au fur et à mesure que le numéro de l'échantillon à traiter sera important. Dans ces conditions, on peut considérer que seul un nombre restreint d'échantillons sont réellement utile pour réaliser l'opération de filtrage.
Ainsi, la formule précédente peut se réécrire ainsi :
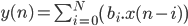
Cette dernière formule est donc bien plus satisfaisante si l'on désire implémenter un filtre en réalité. En effet, il suffit de déterminer une fois pour toute les N coefficients pour l'effet de filtrage choisit et de garder en mémoire les N derniers échantillons. Ce type de filtre est appelé Filtre à réponse impulsionnel fini (filtre RIF).
II. Le filtre à réponse impulsionnelle infinie (RII)
On a vu dans la partie précédente qu'un filtre à réponse impulsionnelle finie est un filtre numérique ayant une forme très simple et qui s'implémente bien sur un microcontrôleur ou sur un PC. Néanmoins, pour effectuer des fonctions de filtrages complexes (avec un ordre élevé), le nombre de coefficient à déterminer et le nombre d'échantillon à stocké peut devenir vite important. Pour ce faire, nous allons voir le filtre à réponse impulsionnelle infini (filtre RII) qui fait entrer en jeu les résultats des filtrages des échantillons précédent.
Nous posons donc directement la formule du filtre RII :
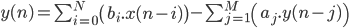
Nous pouvons remarquer que pour calculer la valeur de l'échantillon après filtrage, nous faisons la somme pondéré des N échantillons précédent (jusque là, rien ne change), mais nous rectifions cette somme par la somme des M résultats précédemment obtenus. Implicitement, cette formule rajoute de l'information contenue dans l'ensemble des échantillons depuis le premier jusqu'à l'échantillon courant.
Ce filtre est une formule récursive, on peut la considérer comme une discrétisation d'une équation différentielle linéaire.
L'intérêt d'un tel filtre est qu'il faut garder moins d'échantillon en mémoire qu'un filtre RIF pour obtenir le même effet sur le signal.
D'ailleurs, on peut remarquer que le filtre RIF n'est qu'un cas particulier de filtre RII. C'est le cas où M vaut 0.
III. Réponse impulsionnelle d'un filtre et fonction de transfert
Réponse impulsionnelle par-ci, réponse impulsionnelle par là... mais qu'est-ce donc que ce terme barbare ?
La réponse impulsionnelle d'un filtre est tout simplement le signal obtenu en sortie du filtre lorsque l'on a appliqué une impulsion en entrée. On peut la considérer comme la signature du filtre. Bien souvent, on note la réponse impulsionnelle d'un filtre par la lettre h. Dans le domaine temporel, le signal filtré s'obtient en faisant le produit de convolution du signal non filtré par la réponse impulsionnelle du filtre : 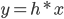
Dans les filtres RIF et RII, la réponse impulsionnelle des filtres est représenté par les coefficients 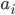 et
et 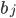
La fonction de transfert quant à elle lie la sortie et l'entrée du filtre. Elle fera donc intervenir la réponse impulsionelle.
Pour calculer la fonction de transfert d'un filtre, on va se placer en représentation fréquentielle grâce à la transformée en Z (cette transformée est utilisée pour obtenir la représentation fréquentielle de signaux discrets. Vous pouvez jeter un œil à cet article pour quelques explications : http://www.ferdinandpiette.com/blog/?p=133)
En fréquentielle, les signaux x et y sont représentés par X et Y, la réponse impulsionnelle h par H et l'opérateur de convolution est remplacé par une multiplication.
On a donc 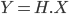 et donc
et donc 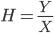 .
.
H est appelé fonction de transfert du filtre.
On peut donc maintenant calculer la fonction de transfert d'un filtre RII.
On a en temporel :
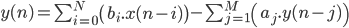
On peut passer cette équation en fréquentielle grâce à la transformée en Z :
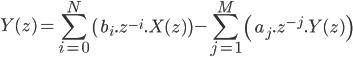
En remaniant un peu cette forme, on obtient :
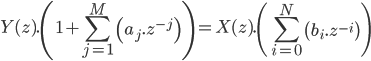
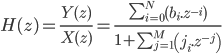
Cette dernière expression est la fonction de transfert d'un filtre RII. Vous trouverez souvent sur internet des fonctions de transfert de filtres numériques sous cette forme. Tout ce qu'il faut faire, c'est d'identifier les différents coefficients afin de pouvoir implémenter ce filtre sur PC ou microcontrôleur.
IV. Du code !!!
Vous trouverez ci-joint du code en C permettant de mettre en place des filtres RIF ou RII.
> Télécharger l'archive .zip
Cette archive contient des sources permettant de mettre en œuvre un filtre numérique. Je l'ai écrit en C pour que quiconque puisse le réadapter pour son besoin (c'est assez bas niveau pour l'implémenter sur microcontrôleur et assez clair pour être recodé dans un langage plus haut niveau (C++ ou autre)).
Vous avez aussi un exemple d'utilisation de la bibliothèque dans le fichier main.c
Cet exemple met en œuvre un filtre passe bas sur un signal échantillonné composé de deux sinus de fréquences 250 et 1500 Hz. Le but étant d'atténuer le second sinus pour n'avoir que le premier.
Voilà le résultat sous forme graphique :
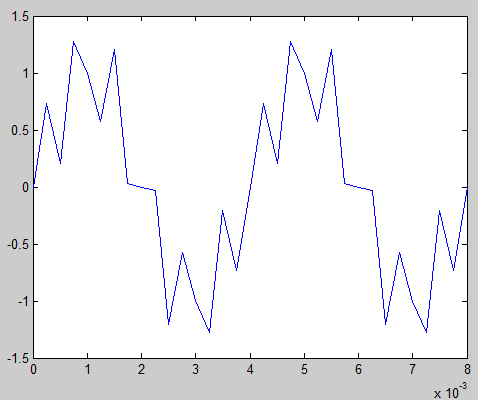
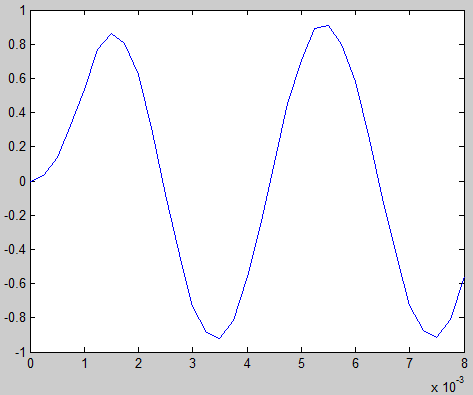

Bonjour,
Merci pour ce partage de connaissance. Des dossiers comme celui-ci permettent d'avancer. Je traite un signal vibratoire issu d'un accéléromètre installé sur un sous-ensemble mécanique tournant. Je cherche à caractériser finement cette vibration. Le signal issu du capteur est échantillonné et convertit en G. Sur la représentation graphique des valeurs en G en fonction du temps, je visualise le motif vibratoire et en estime période et fréquence. L'estimation de la fréquence me permet d'appliquer le théroème de Shannon et ainsi d'améliorer l'échnatillonnage. A partir de ce nouvel échantillonnage, je calcule l'énergie du signal vibratoire. Toujours pour affiner la caractérisation de ce motif, j'aimerais appliquer un filtre tel que décrit dans votre dossier. Mais je ne comprends pas comment en détermner les caractéristiques et calculer la fonction de transfert. Pouvez-vous m'aiguiller svp ?
Bonjour,
Si vous connaissez la fréquence de votre signal, vous pouvez appliquer un filtre passe-bande (analogique sur le signal avant échantillonnage ou numérique sur le signal après) afin de l'isoler. Mais le problème avec cette méthode, c'est que vous coupez toutes les fréquences au delà des fréquences de coupures, donc potentiellement les fréquences de votre motifs présents en second plan (harmoniques et autres).
Si vous êtes sûr que le motif ne contient d'une seule et unique fréquence, alors pourquoi pas.
Dans le cas contraire, ce qui je vous conseillerai plutôt, c'est d'échantillonner votre signal et d'appliquer un technique à base de transformée de Fourier (un périodogramme modifié par exemple) afin de détecter toutes les fréquences utiles de votre motif. A partir de là, il est très facile d'obtenir une estimation de la puissance du signal en fonction des fréquences (voir densité spectrale d'énergie ou de puissance)
Pour en revenir aux filtres, l'article n'explique pas comment calculer la fonction de transfert.
Vous pouvez trouver sur internet des "profils" de fonction de transfert en fonction de vos besoins (Versions numériques des filtres de Butterworth ou de Tchebychev par exemple).
Si vous souhaitez créer vous même votre propre filtre et trouver sa fonction de transfert, c'est beaucoup plus compliqué. Il faudra jeter un œil du côté de la transformée bilinéaire...
Bonjour,
Dans votre code il y a cette formule :
* 0.0408*z + 0.1224*z^-1 + 0.1224*z^-2 + 0.0408*z^-3
* H(z) = ----------------------------------------------------
* 1 - 1.2978*z^-1 + 0.7875*z^-2 - 0.1632*z^-3
*
Pour filtrer des fréquences au dessus de 500hz.
La question est: Si je souhaite avoir une fréquence de coupure quelconque comment calculer les coefficient ai et bi? par exemple si je veux Fc=200hz (fréquence de coupure), quelle est la relation qui lie Fc aux ai et bi pour les déterminer?
Bonjour, pour ça, il faut trouver sur internet des applications qui calculent automatiquement les coefficients en fonction du gabarie souhaité (version numérique de Tchebychev ou de Butterworth).
Calculer à la main les coefficients est un peu fastidieux, il faut utiliser la transformée bilinéaire pour passer une fonction de transfert du domaine continue au domaine discret.
Après, il est tout a fait possible d'écrire un petit script matlab qui calcule ces coefficients en utilisant cet outil mathématique.
Il existe un site qui permet de designer un filtre automatiquement :
http://www-users.cs.york.ac.uk/~fisher/mkfilter/
Merci pour cet article, beaucoup plus agréable à lire que la majorité des articles en ligne que j'ai pu trouver et que j'ai tendance à trouver "gratuitement et scientifiquement barbares". La vulgarisation (quand bien même il n'en s'agisse pas réellement ici) est signe d'une compréhension profonde du sujet par l'auteur !
Merci pour cet article qui m'a permis de comprendre implémentation sur µc,toutefois je me pose deux questions:est-ce bien un filtre d'ordre 3 de Butterworth qui est utilisé avant d'effectuer Tustin?et pour la formule
* 0.0408*z + 0.1224*z^-1 + 0.1224*z^-2 + 0.0408*z^-3
* H(z) = ----------------------------------------------------
* 1 - 1.2978*z^-1 + 0.7875*z^-2 - 0.1632*z^-3
*
le 0.0408*z ne serait pas plutot 0.0408?
Bonjour,
Article très intéressant, bravo.
J'ai une question. Je travail avec un Oculus Rift et les valeurs des positions des controllers/manettes qu'il me retourne sont un peu "saccadé". Pour résoudre ce problème de manière temporaire je fais actuellement une moyenne sur les N dernières positions. Implémenter un filtre passe bas serait-il une bonne idée ? Comment pourrais-je m'y prendre ?
Merci.