Voilà un petit article expliquant l'intérêt d'une transformée de Fourier. Je ferais une partie sur l'implémentation cette transformée et je parlerais des limites d'une telle méthode.
Représentation temporelle VS représentation fréquentielle
Un signal (que ce soit audio, vidéo, ou autre) est souvent représenté sous sa forme temporelle : on a une succession temporelle d'échantillons représentant la valeur du signal à un instant donné. On peut extraire certaines informations directement à partir de cette représentation (amplitude à un instant donné etc.)
Néanmoins, pour analyser un signal, cette représentation temporelle est très limitée ! On ne peut pas avoir accès à des informations de types fréquentielles par exemple. À part dans des cas simples, il nous est donc impossible de dire quelles sont les fréquences présentes dans un signal juste en regardant sa représentation temporelle !
Pour avoir accès à ce genre d'information, il faut représenter le signal sous une autre forme, à savoir sous la forme fréquentielle. Lorsque le signal est représenté sous cette forme, les informations temporelles deviennent inaccessibles mais les informations de fréquences se révèlent au grand jour.
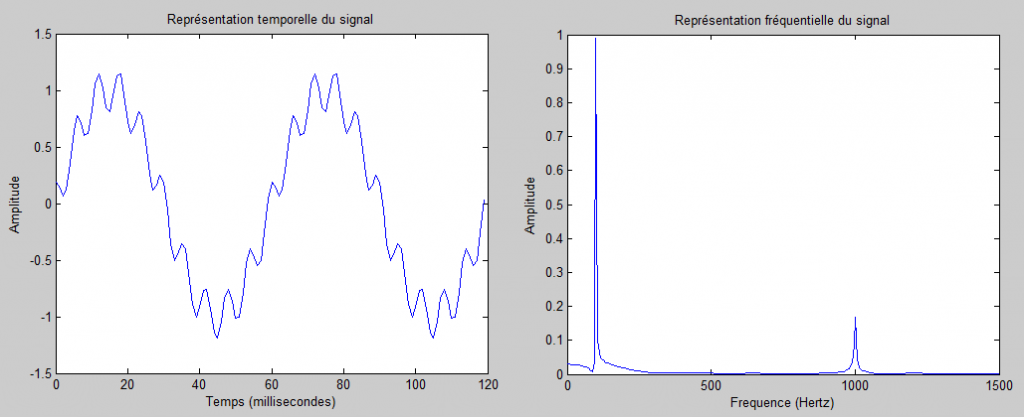
Voilà un exemple de représentation temporelle et fréquentielle d'un même signal (une somme de sinusoïde respectivement de 100Hz à 1Volt d'amplitude et de 250Hz à 0.2V d'amplitude)
Sur la représentation temporelle, on voit bien l'enveloppe temporelle du signal alors que sur la représentation fréquentielle, on voit bien que le signal est bien composé d'une sinusoïde à 100Hz d'amplitude 1 et d'une autre à 1000Hz d'amplitude 0.2.
Bien sûr, ce signal est très simple, mais vous comprenez vite l'intérêt lorsque le signal se complexifie ne serait-ce qu'un peu (la représentation temporelle devient illisible).
La transformée de Fourier
Il existe un moyen de transformer la représentation temporelle d'un signal en sa représentation fréquentielle. Et ce moyen s'appelle la transformée de Fourier.
Aux grands mots, les grands moyens, voici donc la formule de la transformée de Fourier :
Soit un signal 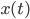 dépendant du temps et sa transformée de fourier
dépendant du temps et sa transformée de fourier 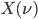 avec
avec 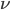 représentant la fréquence, on définie la transformée de Fourier comme
représentant la fréquence, on définie la transformée de Fourier comme
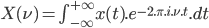
Son expression mathématiques peut sembler un peu complexe à implémenter sur un système réel, mais nous allons voir qu'en réalité, il n'en est rien.
En effet, cette formulation de la transformée de Fourier ne marche que si l'on manipule des fonctions continues dans le temps. Or, en pratique, nous avons quasiment tout le temps des signaux discrets dans le temps (signaux numériques) ! C'est-à-dire que l'on possède la valeur du signal tous les 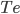 milisecondes par exemple. On ne manipule pas la fonction du signal en elle-même.
milisecondes par exemple. On ne manipule pas la fonction du signal en elle-même.
De ce fait, la transformée de Fourier ne s'applique plus telle quelle. Il faut donc la passer dans le domaine discret. L'intégrale se transforme donc en une simple somme.
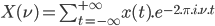
Dans cette formulation, on remarque que l'on doit connaitre tout le signal, de 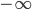 à
à 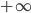 . En réalité, on ne peut pas avoir tout le signal en entier. Bien souvent, on veut analyser seulement une partie du signal de
. En réalité, on ne peut pas avoir tout le signal en entier. Bien souvent, on veut analyser seulement une partie du signal de 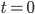 à
à 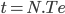 (où Te est la période d'échantillonnage).
(où Te est la période d'échantillonnage).
La formule s'écrit donc
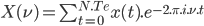
Comme on travaille dans le domaine discret, on peut aussi discrétiser le temps : 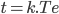 avec
avec 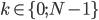 pour un signal de N échantillons
pour un signal de N échantillons
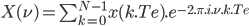
Enfin, comme on a échantillonné le signal en temporelle, le résultat en fréquentielle doit lui aussi échantillonné. On pose donc 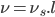 avec
avec 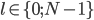 et
et 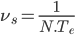 .
.
La valeur de 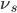 a été choisi afin d'éviter le phénomène de recouvrement temporel.
a été choisi afin d'éviter le phénomène de recouvrement temporel.
Ce qui nous donne la formule finale de la transformée de Fourier discrète (TFD) :
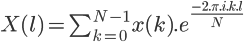
Dans cette formule, on sous-entend que 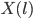 est en réalité
est en réalité 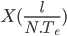 et que
et que 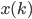 vaut en réalité
vaut en réalité 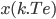
À partir de cette formule, il est donc facile d'implémenter une transformée de Fourier discrète informatiquement.
Implémentation de la transformée de Fourier
Implémentation naïve
L'implémentation naïve de la transformée de Fourier consiste à calculer chaque échantillon fréquentiel à partir de tous les échantillons temporels. Cet algorithme est donc simple à mettre en œuvre, mais possède une complexité importante de l'ordre de 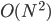 avec N, le nombre d'échantillon du signal. Cet algorithme pédale donc vite dans la choucroute lorsque le nombre d'échantillon à traiter augmente.
avec N, le nombre d'échantillon du signal. Cet algorithme pédale donc vite dans la choucroute lorsque le nombre d'échantillon à traiter augmente.
On peut réécrire la formule de la TFD en version matricielle avec 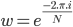 :
:

Ce qui nous donne le pseudo-code suivant :
Fonction TFD(x): pour l = 0 à N-1 X(l) = 0 pour k = 0 à N-1 X(l) = X(l) + x(k) * exponentielle(-2*PI*i*k*l/N) fin pour fin pour
Il faut juste faire attention que le signal X obtenue soit un signal complexe composé d'échantillons complexes (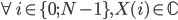 ) ! Pour obtenir l'amplitude du signal dans le domaine fréquentiel, il faut donc prendre le module des X(l) et pour avoir la phase du signal, il faut prendre l'argument des X(l).
) ! Pour obtenir l'amplitude du signal dans le domaine fréquentiel, il faut donc prendre le module des X(l) et pour avoir la phase du signal, il faut prendre l'argument des X(l).
Implémentation rapide
On voit que l'implémentation précédente de la TFD consomme beaucoup de temps de calcul lorsque l'on augmente le nombre d'échantillon à traiter. Il existe une implémentation dite rapide utilisant la récursivité qui permet de diminuer la complexité de l'algorithme en 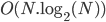 avec N, le nombre d'échantillon. Cette implémentation découle d'une autre formulation de la TDF obtenue en triturant un peu la formulation de base.
avec N, le nombre d'échantillon. Cette implémentation découle d'une autre formulation de la TDF obtenue en triturant un peu la formulation de base.
On part donc de la formulation de la TFD de base vu dans les paragraphes précédents et on remplace 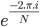 par
par 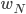 pour des raisons de lisibilités
pour des raisons de lisibilités
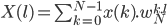
On peut décomposer cette somme en deux sous-sommes. La première somme les échantillons pairs et la seconde les échantillons impairs.
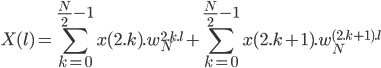
En développant un peu le calcul dans les exponentielles (remplacer 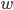 par sa formulation exponentielle pour bien comprendre), on obtient :
par sa formulation exponentielle pour bien comprendre), on obtient :
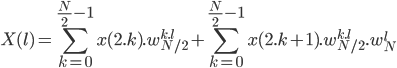
On peut donc sortir de la somme l'exponentielle (le w) ne dépendant que de "l" :
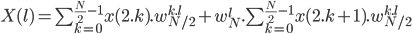
Et là, on remarque que les deux sommes ne sont, en réalité, que les transformées de Fourier discrètes du signal composé des échantillons pairs (noté 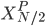 ) et du signal composé des échantillons impairs (noté
) et du signal composé des échantillons impairs (noté 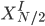 ).
).
On a donc :
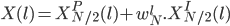
Ici, on détecte un petit problème : comment faire si l est supérieur à 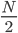 ? Et bien, on applique tout simplement la propriété de périodicité de la transformée de Fourier discrète. Ainsi,
? Et bien, on applique tout simplement la propriété de périodicité de la transformée de Fourier discrète. Ainsi, 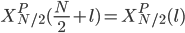
De plus, en développant 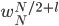 on retombe sur
on retombe sur 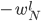
On a donc l'expression récursive de la transformée de Fourier discrète :
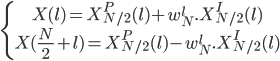
L'intérêt d'une telle formulation se fait particulièrement ressentir quand le nombre d'échantillon N est une puissance de 2. En effet, dans ce cas, on peut diviser la liste des échantillons en 2 parties (d'indices pairs et d'indices impairs) par récursion jusqu'à ce que la liste en question ne contienne plus qu'un élément. Dans ce cas-là, la transformée de Fourier du signal à un seul échantillon est égal à l'échantillon lui-même.
Cet algorithme est d'une complexité 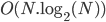 comparé à l'algorithme naïf qui lui est en
comparé à l'algorithme naïf qui lui est en 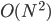 . Pour 16384 échantillons, le gain de temps est de l'ordre de 1000 !!
. Pour 16384 échantillons, le gain de temps est de l'ordre de 1000 !!
Voilà le pseudo-code de la transformée de Fourier rapide :
Fonction FFT(x):
pour i de 0 à N/2-1
x_pair(i) = x(2*i)
x_impair(i) = x(2*i+1)
fin pour
si N/2 = 1
X_pair(0) = x_pair(0)
X_impair(0) = x_impair(0)
sinon
X_pair = fft(x_pair)
X_impair = fft(x_impair)
fin si
pour i = 0 à N/2-1
X(i) = X_pair(i) + X_impair(i) * exponentielle(-2*pi*i/N)
X(N+i) = X_pair(i) - X_impair(i) * exponentielle(-2*pi*i/N)
fin pour
J'ai codé les deux algorithmes en C et le gain de temps est bien celui escompté. Pour 16284 échantillons (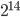 ), l'algorithme naïf met 2 minutes à calculer la TFD alors que l'algorithme rapide ne met que 125 milisecondes.
), l'algorithme naïf met 2 minutes à calculer la TFD alors que l'algorithme rapide ne met que 125 milisecondes.
Utilisation et limites de la transformée de Fourier
La transformée de Fourier permet d'obtenir une représentation fréquentielle d'un signal stationnaire. Et c'est bien là le problème. On ne peut pas analyser un morceau de musique avec une TFD simple. En effet, on perdrait l'information temporelle.
Par exemple, si on a deux signaux. Le premier composé d'une sinusoïde à 100Hz pendant une seconde puis d'une sinusoïde à 200Hz pendant une seconde. Et le second composé d'une sinusoïde à 200Hz pendant une seconde et d'une à 100Hz pendant la seconde suivante. Et bien leurs transformées de Fourier respectives seront identiques.
La TFD s'utilise donc uniquement sur des signaux dont l'on sait que l'information fréquentielle est la même partout. Autrement, on utilise d'autres méthodes qui permettent d'obtenir une représentation fréquentielle et temporelle en même temps comme la transformée de Fourier à fenêtre glissante, les distributions de la classe de Cohen (comme la distribution de Wigner-Ville), ou la transformée par ondelettes, etc.
De plus, les signaux que l'on veut analyser sont dans la plupart des cas bruités. Ce que l'on cherche alors, c'est une estimation de la répartition énergétique du signal en fréquence. La TFD ne peux plus s'appliquer telle quelle. On doit utiliser des estimateurs spécifiques comme l'estimation par corrélogramme ou par périodogramme (qui utilisent la TFD).
Remarques : la transformée de Fourier inverse
La transformée de Fourier permet de passer du domaine temporel au domaine fréquentiel. L'inverse est tout aussi possible. On peut passer du domaine fréquentielle au domaine temporel en appliquant une transformée de Fourier inverse.
Voici sa forme continue : 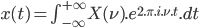
Et voilà sa forme discrète : 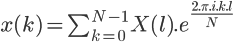

Tres bon cours. Merci
Pour la transformée de Fourier inversé, n'aurait-il pas plutôt fallut le faire en fonction de ν et non t?