Afin d'illustrer les deux premiers articles du dossier sur la logique flou, je vous présente dans cet article un système flou relativement simple permettant de planifier une trajectoire d'un robot mobile. Le but du système flou sera de décider de la vitesse des deux roues du robot afin que celui-ci ne percute aucun obstacle. Aucun objectif ne sera programmé. Tout ce que l'on souhaite, c'est que le robot puisse se déplacer aléatoirement sans percuter aucun obstacle tout en ayant une trajectoire fluide.
I Le robot
Le robot sur lequel sera implémenté le système flou est un robot très basique. Il possède deux roues motorisés plus une roue libre ainsi que trois systèmes de capteurs permettant de déterminer la distance du robot aux obstacles situés en face, à droite et à gauche. Par exemple, dans notre système, les capteurs peuvent être trois capteurs ultrason d'une portée maximale de 3.5 ou 4 mètres.
Le but du système flou, c'est de déterminer la vitesse des roues droite et gauche en fonction de la distance des obstacles autour du robot.
II Les variables linguistiques
La première étape est donc de déterminer les variables linguistiques d'entrées et de sorties.
En entrée, on a les distances du robot aux obstacles de devant, de gauche et de droite. Dans notre système, j'ai donc choisi deux variables linguistiques afin de représenter une donnée distance : la variable distance_petite et distance_grande.
En sortie, on veut les vitesses des roues du robot. Pour l'exemple, une vitesse d'une roue est représenté par un rapport cyclique de signal PWM. Ce rapport est compris entre 0 et 1. Les variables linguistiques choisies pour qualifier ce rapport cyclique sont vitesse_petite, vitesse_moyenne et la variable vitesse_grande.
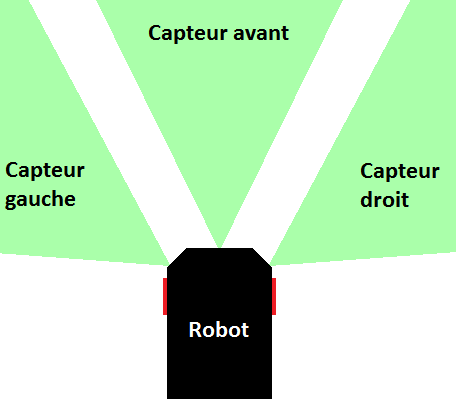
Maintenant que l'on a nos variables linguistiques d'entrées et de sorties, il nous faut choisir des fonctions d'appartenances. Une distance est dite petite si elle est inférieure à un mètre et grande si elle est supérieure à trois mètres. Le rapport cyclique est petit s'il est nul, moyen s'il vaut 0.5 et grand s'il vaut 1. Les fonctions d'appartenances sont donc très simples.
Ici, les fonctions d'appartenances pour le rapport cyclique sont particulières puisqu'une variable linguistique ne représente qu'une seule valeur de rapport cyclique. Cela va permettre de simplifier grandement les calculs lors de la défuzzification puisqu'un simple calcul de barycentre remplacera un calcul complexe de centre de gravité.
Remarque : Bien sûr, je n'ai choisi que deux variables linguistiques par données d'entrée et trois par donnée de sortie pour l'exemple, mais rien ne vous empêche d'en choisir plus !
III Les règles d'inférences
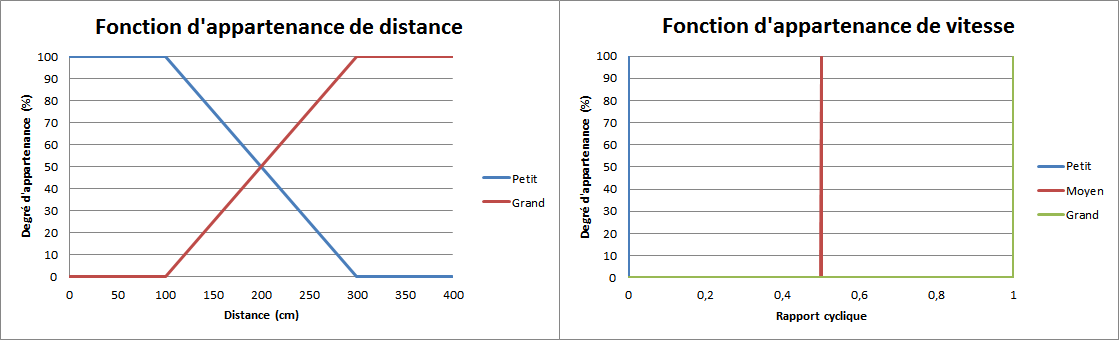
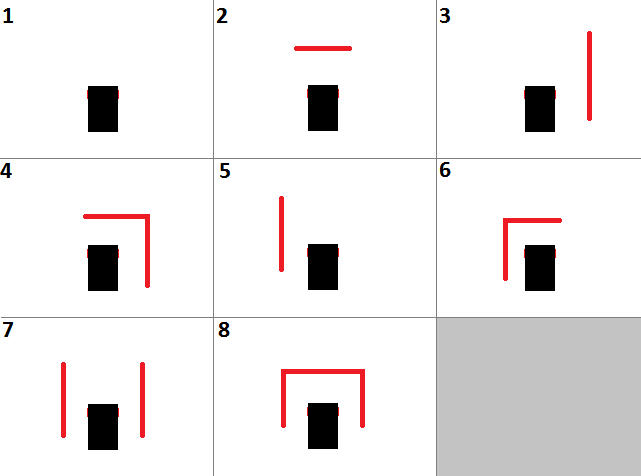
Dans notre cas, ayant trois capteurs avec deux variables linguistiques par donnée capteur, on aura au maximum 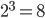 règles d'inférences qui correspondent aux 8 cas suivant :
règles d'inférences qui correspondent aux 8 cas suivant :
Cas un :
Le premier cas, c'est le cas où aucun obstacle n'est détecté. Dans ce cas-là, on veut aller tout droit à pleine vitesse.
Cas deux :
Ici, si on a un obstacle devant, mais rien sur les côtés, alors il faut tourner. Au hasard, on choisira de tourner à droite. Il faut donc une grande vitesse sur la roue gauche et une petite sur la roue droite.
Cas trois :
Si un obstacle est présent uniquement à droite, alors on tourne légèrement à gauche. La vitesse de la roue droite sera grande alors que celle sur la roue gauche sera moyenne.
Cas quatre :
Si on a détecte un obstacle à droite et devant, alors on tourne fortement à gauche. La vitesse de la roue droite sera grande et celle de la roue gauche sera petite.
Cas cinq :
Si on détecte un mur à gauche, il faudra tourner légèrement à droite. La vitesse de la roue gauche sera grande alors que celle de la roue droite sera moyenne.
Cas six :
En présence d'un mur à gauche et devant, on tournera fortement à droite. La vitesse de la roue gauche sera grande et celle de la roue droite, petite.
Cas sept :
Si la voie est libre en face, mais qu'il y a deux obstacles de chaque côté du robot, alors on avance prudemment. La vitesse des deux roues sera moyenne.
Cas huit :
Enfin, si le robot détecte des obstacles proches sur tous les capteurs, alors il devra faire demi-tour. Au hasard à droite. La roue gauche tournera à grande vitesse alors que la roue droite aura une vitesse petite.
Les règles d'inférences seront donc :
- SI distance_gauche = grande ET distance_avant = grande ET distance_droite= grande ALORS vitesse_gauche = grande ET vitesse_droite = grande
- SI distance_gauche = grande ET distance_avant = petit ET distance_droite = grande ALORS vitesse_gauche = grande ET vitesse_droite = petite
- SI distance_gauche = grande ET distance_avant = grande ET distance_droite = petit ALORS vitesse_gauche = moyenne ET vitesse_droite = grande
- SI distance_gauche = grande ET distance_avant = petit ET distance_droite = petit ALORS vitesse_gauche = petite ET vitesse_droite = grande
- SI distance_gauche = petit ET distance_avant = grande ET distance_droite = grande ALORS vitesse_gauche = grande ET vitesse_droite = moyenne
- SI distance_gauche = petit ET distance_avant = petit ET distance_droite = grande ALORS vitesse_gauche = grande ET vitesse_droite = petite
- SI distance_gauche = petit ET distance_avant = grande ET distance_droite = petit ALORS vitesse_gauche = moyenne ET vitesse_droite = moyenne
- SI distance_gauche = petit ET distance_avant = petit ET distance_droite = petit ALORS vitesse_gauche = grande ET vitesse_droite = petite
IV La défuzzification
Avant de défuzzifier, il faut n'avoir qu'une variable linguistique de chaque type (à savoir six variables linguistiques au total, trois par roue). Pour ça, on décide de faire la disjonction des règles :
- règle_1 OU règle_2 OU règle_3 OU règle_4 OU règle_5 OU règle_6 OU règle_7 OU règle_8
Une fois que l'on a nos six variables linguistiques, il suffit d'appliquer un calcul de barycentre sur chacune des variables linguistiques afin de déterminer les rapports cycliques des roues droite et gauche.

V Le choix des opérateurs
Maintenant que l'on a toutes les étapes de notre système flou, il ne nous reste plus qu'a choisir les opérateurs que l'on souhaite utiliser.
Ici, on ne va pas se compliquer la vie, on va choisir :
- L'opérateur de minimalité pour le ET au sein des règles
- L'opérateur de maximalité pour le OU entre les règles
VI Exemple
Testons notre système sur un exemple. Supposons qu'à un instant donné, les capteurs nous renvois les valeurs suivantes :
- Capteur gauche : 130 centimètres
- Capteur avant : 240 centimètres
- Capteur droite : 350 centimètres
La première étape est l'étape de fuzzification.
- distance_gauche = petit à 85% et grand à 15%
- distance_avant = petit à 30% et grand à 70%
- distance_droite = petit à 0% et grand à 100%
Ensuite, on applique les règles d'inférences :
- règle_1 : vitesse_gauche_grande = vitesse_droite_grande à 15 %
- règle_2 : vitesse_gauche_grande =vitesse_droite_ petite à 15%
- règle_3 : vitesse_gauche_moyenne = vitesse_droite_grande à 0%
- règle_4 : vitesse_gauche_petite = vitesse_droite_grande à 0 %
- règle_5 : vitesse_gauche_grande = vitesse_droite_moyenne à 70 %
- règle_6 : vitesse_gauche_grande = vitesse_droite_petite à 30 %
- règle_7 : vitesse_gauche_moyenne = vitesse_droite_moyenne à 0 %
- règle_8 : vitesse_gauche_grande = vitesse_droite_petite à 0 %
On fusionne les variables linguistiques en utilisant l'opérateur maximalité du OU logique :
- vitesse_gauche_grande = 70%
- vitesse_gauche_moyenne = 0%
- vitesse_gauche_petite = 0%
- vitesse_droite_grande = 15%
- vitesse_droite_moyenne = 70%
- vitesse_droite_petite = 30%
Enfin, on défuzzifie :
- rapport_cyclique_gauche = ( 70% * 1 + 0% * 0.5 + 0% * 0 ) / 70% = 1
- rapport_cyclique_droit = (15% * 1 + 70% * 0.5 + 30% * 0) / 115% = 0.43
On obtient donc notre rapport cyclique final pour chacune des roues. Avec cette configuration, le robot tournera sur la droite. En effet, il y a un obstacle proche à gauche et à moyenne distance devant.
VII Remarques
Cet exemple de planification de trajectoire est extrêmement simple. Non seulement au niveau des variables linguistiques et de leurs fonctions d'appartenances, mais aussi au niveau des opérateurs logiques utilisés. Rien ne vous empêche de complexifier ce modèle vous-même en :
- Rajoutant des variables linguistiques pour qualifier la distance
- Rajouter des variables linguistiques au niveau du rapport cyclique afin de gérer la marche arrière des roues du robot (dans notre exemple, une roue ne peut tourner que dans un seul sens)
- Rajouter des capteurs
- Modifier la forme des fonctions d'appartenances d'entrées et de sortie
- Modifier la façon dont l'on défuzzifie les variables linguistiques de sorties
- Modifier les opérateurs logiques utiliser
Bref, tout est entièrement customisable. C'est là tout l'intérêt des systèmes flous.

Magnifique dans la simplicité des explications ^^ Kokosy serait fière jeune Padawan !
Bonjour et merci déjà pour cet exemple. je désire faire de l'évitement d'obstacle avec un robot mobile à deux roues en utilisant la commande floue. cependant j'ai quelques difficultés.
1- comment faire la poursuite d'une trajectoire?
2- comment faire la simulation avec matlab?
si vous disposez d'informations faites moi signe s'il vous plait. cordialement, Ully.
Bonjour,
Pour atteindre un point objectif, vous pouvez par exemple coupler un système flou qui va permettre d'éviter les obstacles, avec un système de champs de potentiel où l'objectif serait un point attractif.
Cet article devrait vous intéresser : http://www.ferdinandpiette.com/blog/2011/05/algorithmes-de-planification-de-trajectoires-bref-etat-de-lart/
Pour se qui est de la simulation sous matlab, je n'en ai aucune idée.
Cordialement,
Ferdinand
Bonjour,
Bravo pour ton site bien rédigé. C'est toujours une source d'inspiration
Il y a une petite faute d'intention dans la première règle d'inférence : .
Pour ceux qui souhaitent voir une simulation du planificateur décrit ci-dessus :
Fuzzysimu sur Github
Bonsoir,
Merci pour ton commentaire.
J'ai corrigé la boulette 😉
Bonne soirée.
Is there any MATLAB program for FUZZY LOGIC, without using TOOLBOX, I want to get the final curve before defuzzification step?
bonjour merci pour ton exemple
je peut avoir la programmation de cet exemple en C ou java
et merci pour votre aide
Bonjour, comment implementer cette commande floue sur un uC de type pic s'il vous plait.en language C je veux dire.
Merci
j ai besoin d'une suite d'un programme matlab pour évitements d'obstacle d'un robot mobile en sachant que j'ai utilisé l’algorithme pso(optimisation par essaim de particules).
merci