Lorsque vous souhaitez appliquer un filtre de Kalman pour estimer des paramètres d'un système, la première chose à faire est de modéliser votre problème. Il se trouve que dans certain cas, les équations qui permettent de modéliser le problème ne sont pas linéaires. De ce fait, le filtre de Kalman n'est plus applicable tel quel. Heureusement, il est tout de même possible d'estimer les paramètres du système à l'aide d'un filtre de Kalman dit étendu. Ce filtre permet en effet de linéariser localement le problème et donc d'appliquer les équations du filtre de Kalman classique.
Dans cet article, je vais donc vous décrire le fonctionnement d'un filtre de Kalman étendu, puis je reprendrais l'exemple de l'article http://www.ferdinandpiette.com/blog/2011/04/exemple-dutilisation-du-filtre-de-kalman/ afin d'utiliser un EKF (Extended Kalman Filter).
Pour pouvoir lire cet article, vous devez être familié avec le filtre de Kalman classique. Je vous conseille donc de lire la série de trois articles sur le filtre de Kalman que vous trouverez sur ce site : http://www.ferdinandpiette.com/blog/2011/04/premiers-articles-du-blog/
EKF : Le fonctionnement
Le principe d'un filtre de Kalman étendu est très simple. Tout d'abord, les équations d'état et les équations liant l'état précédent à l'instant suivant qui étaient linéaires dans le cas du filtre de Kalman classique sont maintenant non linéaire. Il est donc impossible de l'écrire sous forme matricielle.
On remplace donc les équations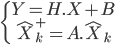 
par 
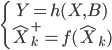
On est donc obligé d'appliquer ces équations non linéaires pour le calcul de la prédiction et la mise à jour du vecteur d'état. Les équations de Kalman deviennent donc :
La phase de prédiction
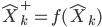
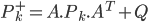
La phase de mise à jour
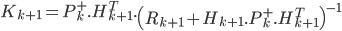
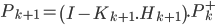
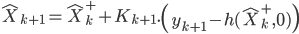
Vous remarquerez que pour mettre à jour le vecteur d'état, on utilise l'équation d'état non linéaire avec un bruit nul (second paramètre de la fonction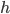 
à 0).
Il reste un problème en ce qui concerne le calcul de la covariance de l'erreur et du gain de Kalman. En effet, on utilise toujours les matrices d'observation et de transition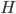 
et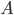 
. Pour pouvoir utiliser ces formules, il faut donc que l'on linéarise localement les fonctions 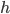et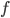 
. On obtient donc les matrices d'observation et de transition en prenant les matrices des dérivés partielles des équations non linéaires (aussi appelé Jacobiennes).
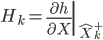
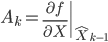
Avec ces Jacobiennes, il est donc possible d'appliquer le filtre de Kalman tel que défini ci-dessus. Il suffit de recalculer les matrices aux dérivées partielles à chaque nouveaux échantillons à traiter et d'utiliser ces matrices dans les équations.
Par contre, on se rend bien compte que l'on linéarise localement les équations afin d'appliquer le filtre de Kalman. Cette linéarisation est locale, ce qui entraine donc une convergence locale du filtre de Kalman étendu. Ce filtre ne garantis donc pas une convergence globale (à l'inverse du filtre de Kalman classique). La stabilité d'un EKF est donc plus difficile à garantir et dépend souvent de sa bonne initialisation.
EKF : Exemple
Pour mieux comprendre le filtre de Kalman étendu, nous allons reprendre l'exemple présenté ici : http://www.ferdinandpiette.com/blog/2011/04/exemple-dutilisation-du-filtre-de-kalman/
Pour rappel, nous cherchions à estimer la vitesse angulaire et l'angle d'un mobile supposé sans accélération à l'aide d'un accéléromètre et d'un gyroscope en prenant en compte le phénomène de dérive du gyroscope. Afin d'avoir un filtre de Kalman linéaire, nous avions appliqué un traitement sur les échantillons de l’accéléromètre afin de les convertir en angle avant d'appliquer le filtre de Kalman. Maintenant, nous allons essayer d'appliquer le filtre de Kalman étendu directement sur la valeur de l'accélération. La conversion de l'accélération en angle (qui est une opération non linéaire (présence d'un sinus)) va donc être intégré au filtre de Kalman.
Il nous faut donc modéliser le nouveau système. Le vecteur d'état à estimer est toujours le même. Il s'agit de la vitesse angulaire (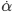
), de l'angle du mobile (
) et du biais du gyroscope (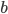
). Le vecteur de mesure quant à lui change. Il sera composé de la vitesse angulaire récupéré du gyroscope (
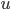) et de l'accélération fournis par l'accéléromètre (
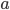) (et non plus l'angle donné par l'arc sinus du rapport de l'accélération par la constante de gravitation g).
On pose donc les équations d'états (non linéaires) :
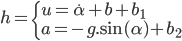
Ainsi que les équations de transitions (qui sont linéaires) :
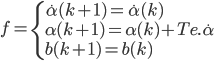
Maintenant, il faut calculer les Jacobiennes de ces systèmes d'équations. Commençons par la Jacobienne des équations d'états.
Vu que f est un système d'équation linéaire, la Jacobienne de f sera égale à la matrice A de l'exemple du kalman linéaire.
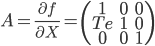
Les matrices de covariance du bruit de mesure et de covariance du bruit de commande sont les mêmes que pour l'exemple du filtre de Kalman linéaire.
Maintenant que le système est entièrement modélisé, on peut donc appliquer les équations du filtre de Kalman étendu.
1- En premier lieu, il faut recalculer la Jacobienne des équations de transitions à l'aide du vecteur d'état précédent estimé. (Dans notre cas, la Jacobienne ne change pas car les équations de transitions sont linéaires).
2- Ensuite, on applique la phase de prédiction.
3- On recalcule la Jacobienne des équations d'états à l'aide du vecteur d'état prédit. (on utilise donc le de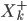 
afin de calculer 
).
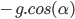4- Enfin, on applique la phase de mise à jour.
Les performances de ce filtre sont équivalentes à la modélisation linéaire présenté dans l'exemple précédent.
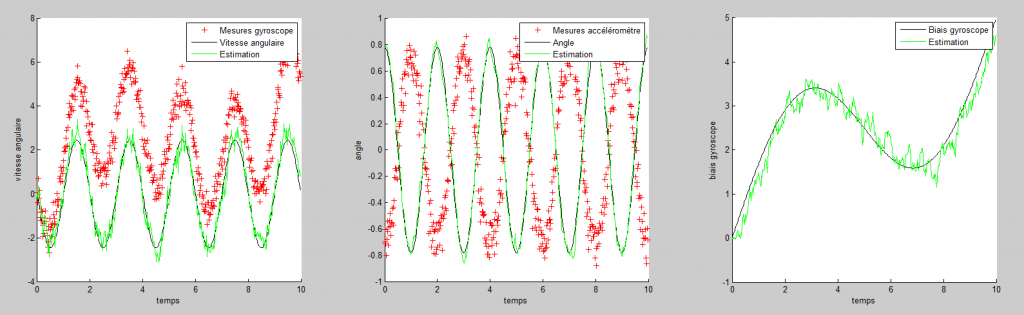(Vous remarquerez que dans cette simulation, j'ai fourni l'accélération non pas en mètre par seconde carré, mais directement en g)
Conclusion
Le filtre de Kalman étendu permet donc de linéariser localement des systèmes non linéaire. Ceci assure donc la convergence locale de l'erreur, mais non celle globale. Un surcoût de calcul est constaté par rapport au filtre de Kalman classique. En effet, outre les opérations non linéaires introduit dans les équations d'états et de transitions, il faut recalculer à chaque étape les Jacobiennes de ces équations.
bonjour, je vous remercie pour ce cours détaillée du filtre de kalman étendu. Pourriez vous m'envoyé le code source de l'exemple que vous avez présenter pour mieux comprendre 🙂
merci infiniment
Bonjour,
J'ai juste une question concernant l'exemple. Comment linéariser h(X) dans l'équation de mesure Y ? Je comprend comment on calcule la matrice des jacobiennes H qui nous sert ensuite au calcul du gain mais je ne vois pas comment linéariser h(X).
Merci d'avance.
Bonjour.
C'est la matrice Jacobienne qui te permet de faire une approximation linéaire locale de ton système.
Si tu prend comme exemple une fonction F(x)
Pour x ~= M
F(x) = F(M) + J(M).XM + erreur
Avec F une fonction, J sa jacobienne et XM un vecteur.
Dans cette exemple, tu as réussi à linéariser F en utilisant la jacobienne de cette fonction.
Dans le filtre de Kalman Étendu, il te suffit juste de calculer la matrice Jacobienne H de ton système h(X) et de remplacer h(X) dans tes équations par H, la matrice jacobienne.
Le fait de remplacer h(X) par sa jacobienne H linéarise localement ton système.
Bonjour,
Merci pour cette approche pratique de ce filtre.
Je me suis perdu à la 2eme ligne 😳 mais je pense avoir besoin de ce genre de filtre car je fais l'acquisition de données à peu près échantillonnées à intervalles réguliers ce qui génère pas mal de bruit.
Je dois mettre en œuvre un filtrage des données rapide car j'utilise ces données en directe pour une machine mouvante donc je voudrais limiter les bruits qui entraineraient des vibrations.
Je n'ai pas vu sur votre blog la mise en code de ce type de filtrage .
Cordialement
Bonjour,
Je me demande s'il y a un moyen efficace pour trouver le valeur des matrices des covariances?
Merci d'avance
Cordialement
Bonjour,
Je te conseille de lire les commentaires des articles précédents pour avoir la réponse.
merci pour vos explications,
comme d'autres remarques je pense qu'il serait sympa de fournir le .m du kalman étendu car
votre fichier .m du filtre de kalman simple m'a permis sa compréhension.
cordialement.
Bonjour,
Je vous remercie de vos explications dans cet article.
Dans mon sujet de thèse, j'utilise le filtre de kalman dans le but de tracker et d'estimer les mouvements d'un véhicule. Dans le but de tester l'utilisation de filtre de kalman linéaire, j'ai pris l'hypothèse que la direction du véhicule est constante et la capacité de braquage n'évolue pas en fonction du temps (les équations du mouvement cinématique du robot unicycle).
Mais en réalité, je dois utiliser le filtre de kalman étendu pour intégrer la direction et la capacité de braquage du véhicule et nous devons estimer tout comme la position (x,y), la vitesse (vx et vy) du véhicule et l'angle d'orientation tetha (c'est-à-dire considérer non plus le mouvement d'un robot unicycle mais plus un tricycle).
Après avoir modéliser les équations de déplacement du véhicule, je connais quelques difficultés à la mise en place des équations de kalman et comment faire les jacobiennes dans ce cas précis. S'il vous plait, auriez-vous une idée de la manière de procéder?
Cordialement
bonjour
moin aussi dans ma thése sur la securite des réseaux vanet, je cherche a modéliser les équations de déplacement du véhicule, pouriez vous me dire comment avez vous fait pour modeliser la dynamique d'une voiture (documentation) et merci.
cordialement
Bonsoir,
tout d'abord je vous remercie pour cette article vraiment il ma aidé sur mon projet de fin d'étude, dans mon sujet sa concerne la localisation d'un terminal mobile basé sur le filtre de Kalman étendu, avant de faire le programme pour estimer la position du mobile j'ai crée la matrice jacobienne (H), mais le problème est que j'ai des difficultés sur la mise en place des équations d'estimation, auriez vous une aidé de la manière de procédé ou bien des articles qui peuvent être utile ?
cordialement.
Merci pour votre travail, pourriez-vous m'envoyer le code Matlab de l'exemple comme c'était fait pour le filtre Kalman classique
Bonjour,
Je vous remercie pour cet article. En fait, le système de mon travail est l'IMU(3 gyro et trois accelo) est un système non linéaire. Donc je vais essayé d'utiliser le filtre de kalman étendu. Etant donné que je suis débutante,
s'il vous plait, est ce que vous pouvez m'envoyer le code source.
Et merci d'avance!
bonjour
merci pour les explications. pourrions nous avoir un code
cordialement ?
bonjour
je me demande s'il y a un programme de filtre de kalman étendu sur matlab svp 😀
merci
bonjour,
pouvez vous nous présenté le filtre de Kalman sans parfum UKF ?
Bonjour,
J'ai bien compris toutes vos explications. Mon sujet de thèse porte sur un UAV à voilure fixe. J'utilise pour mon test en vol un capteur IMU et un GPS. Etant donné que mon système est non linéaire, je suis parti sur un EKF. J'ai déjà linéarisé et discrétisé les matrices de mes équations d'états mais je rencontre des difficultés lors de l'implémentation sur matlab. Donc je pense que votre code sera d'une grande aide. Serait-il possible de l'obtenir ?
Bonjour,
Je suis actuellement à BAC+3 en école d'ingénieurs et j'ai actuellement à dimensionner un filtre de Kalman dans le but de récupérer l'accélération, vitesse, ... d'un système en mouvement (petit robot).
Pourriez-vous me communiquer, par privé, vos coordonnées car j'ai des petites questions à vous poser.
Merci d'avance.
Bonjour Ferdinand,
J'ai implémenté avec succès ce filtre dans un de mes projets Python en remplacement d'un simple filtre complémentaire! Et ce grâce à toi donc d'abord merci!
Voici un petit retour d'un problème que j'ai eu en le faisant: le filtre avait l'air de partir dans le sens opposé par rapport a mon filtre complémentaire et malheureusement ce n'était pas une erreur de signe. J'ai rajouté une lecture sur un axe de mon accéléro' et donc j'ai ajouté une ligne aux équations d'état "h". avec le cosinus au lieu du sinus. J'ai adapté les matrices qu'il fallait adapter (H et R entre autres) et le filtre converge désormais et suit à peu près mon filtre complémentaire!
Voilà tout, si ça peut aider quelqu'un ...
A+!
Bonjour,
Vos explications sur le kalman en version linaire et EKF sont vraiment intéressantes.
Afin de bien identifier les différences entre l'EKF par rapport à la version classique, avez vous possibilités de transmettre votre code matlab EKF svp.
Merci d'avance