Dans cet article, je vais décrire un peu plus en détail la conception et fonctionnement d'un système flou. Je vais commencer par présenter les trois parties d'un système flou (fuzzification, moteur d'inférences et défuzzification). Je détaillerais ensuite chacune de ces trois parties. Je proposerais enfin un exemple simple afin d'illustrer un peu cet article.
Si vous n'avez jamais entendu parlé de logique floue avant maintenant, je vous conseille de lire cet article qui explique un peu le principe de la logique floue, ses avantages, ses inconvénients et les domaines d'applications de cette théorie : La logique floue : Intérêts et limites
Le fonctionnement d'un système flou
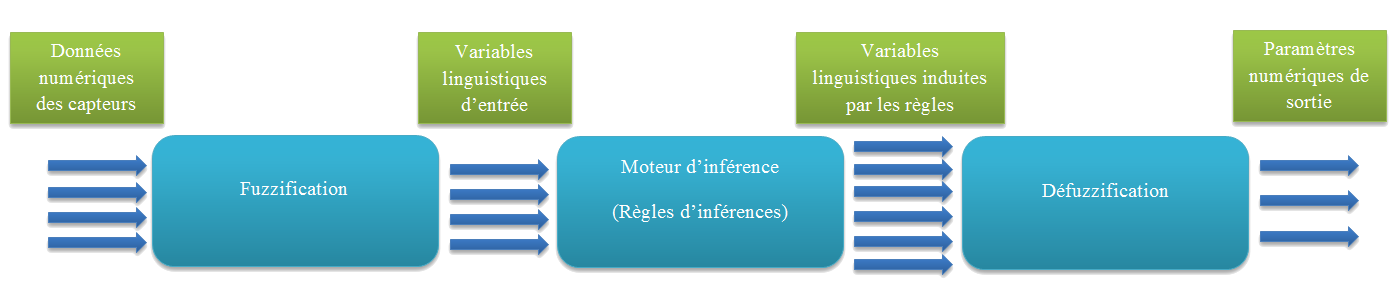
Le principe d'un système flou, c'est de pouvoir calculer des paramètres de sorties en fournissant au système un ensemble de règles formulés en langage naturel. Pour qu'il y ait comptabilités entre les données capteurs, ces règles et les paramètres de sortie, on doit décomposer un système flou en trois parties.
La première partie qui permettra de traduire une donnée numérique provenant d'un capteur en une variable linguistique s'appelle la fuzzification. Grâce à une fonction d'appartenance créée par le concepteur du système flou, on va pouvoir transformer une donnée capteur quantitative en variable linguistique qualitative (par exemple, une donnée provenant d'un capteur pourrait être distance=10.56 mètre. Après fuzzification, on aurait donc distance=30%proche, 50%moyen, 20%loin)
La seconde partie est le moteur d'inférence qui se chargera d'appliquer chacune des règles d'inférences. Ces règles d'inférences représentant les connaissances que l'on a du système dû à l'expertise humaine. Chaque règle génèrera une commande de sortie.
Enfin, la troisième étape est la défuzzification. C'est l'étape permettant de fusionner les différentes commandes générés par le moteur d'inférence pour le donner qu'une seule commande de sortie et de transformer cette variable linguistique de sortie en donnée numérique.
La fuzzification
L'étape de fuzzification à pour but de transformer une donnée numérique en variable linguistique. Pour cela, le concepteur du système flou doit créer des fonctions d'appartenances. Une fonction d'appartenance est une fonction qui permet de définir le degré d'appartenance d'une donnée numérique à une variable linguistique.
Prenons par exemple une température en degré Celcius provenant d'un capteur. On veut transformer cette donnée numérique en variable linguistique. On peut trouver plusieurs variables linguistiques qualifiant une température : chaud, froid, très froid, tempéré, très chaud, etc.
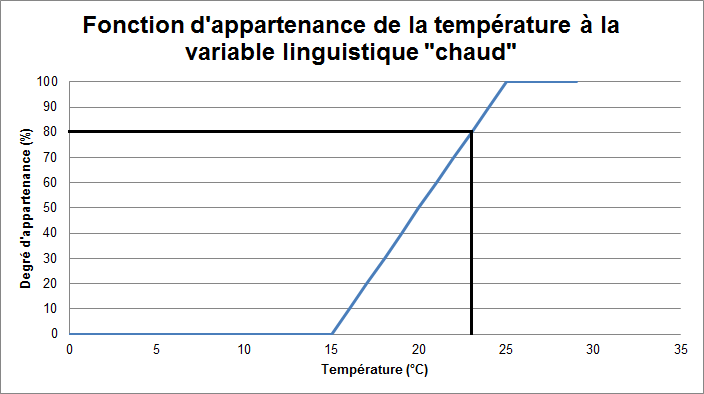
Maintenant, il suffit de créer une fonction d'appartenance de la température à chacune de ces variables. Créons la fonction d'appartenance de la température à la variable linguistique "chaud"
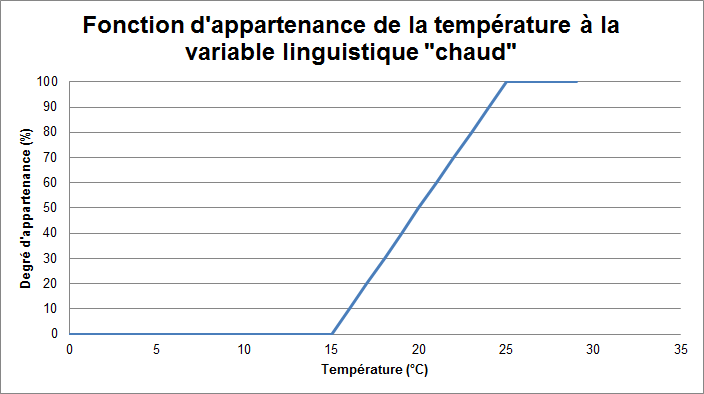
Ici, si notre capteur de température nous indique 23°, la fuzzification nous dira que la température est chaude à 80%.
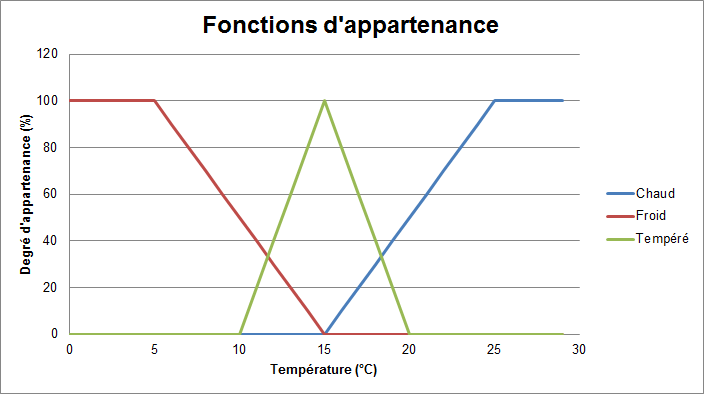
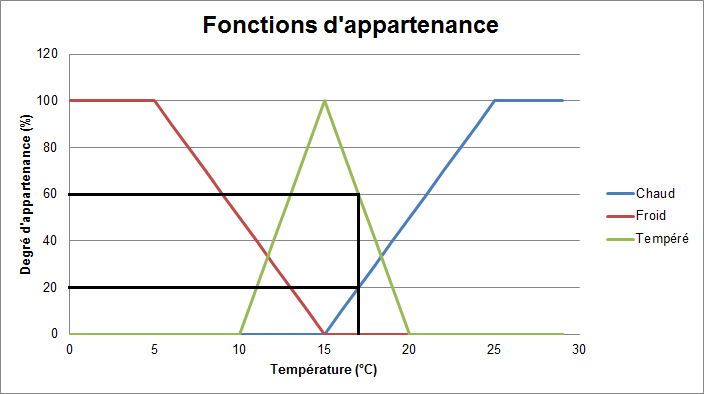
Bien évidemment, on peut utiliser plusieurs variables linguistiques pour caractériser un seul type de données. Ici, nous choisirons trois variables linguistiques pour qualifier la température : chaud, froid et tempéré.
Pour cela, il faut créer une fonction d'appartenance pour chaque variable. Comme ces fonctions d'appartenances qualifient un même type de données, on peut les représenter sur le même graphique.
Si le capteur nous renvoie 17°C, après fuzzification, la température sera chaude à 20%, tempérée à 60% et froide à 0%.
Pour l'exemple, on a choisi des fonctions d'appartenances relativement simples. Elles sont linéaires ou en forme de triangle. Mais libre au concepteur du système de choisir une fonction d'appartenance plus complexe s'il estime que le gain de performance est non négligeable. Les fonctions d'appartenances les plus courantes ont une forme de triangle, de trapèze ou de cloche.
Par ailleurs, on remarque que si l'on choisit une fonction d'appartenance en forme de rectangle, ou une fonction de Heaviside, on se retrouve dans le cas d'une logique classique !!
Cette première étape de fuzzification va donc traduire les données numériques des capteurs en différentes variables linguistiques.
Le moteur d'inférence
Maintenant que l'on possède des variables linguistiques, on va pouvoir les passer dans le moteur d'inférence. Ici, chaque règle du moteur d'inférence est écrite par le concepteur du système flou en fonction de connaissance qu'il possède. La première chose à faire pour cette seconde partie est donc de lister toutes les règles que l'on connait et qui s'applique au système.
Une règle doit être sous la forme Si condition, alors conclusion.
Par exemple, SI la vitesse est grande ET la distance au feu est courte ALORS freine fort, est une règle d'inférence valide.
Le problème dans les règles d'inférences, c'est de savoir ce que les opérateurs logiques signifies. En effet, les opérateurs de la logique classique (ET, OU) ne sont plus valables en logique floue. Il faut donc les redéfinir nous-même.
L'opérateur ET (T-Norme)
L'opérateur ET en logique floue correspond à l'intersection de deux ensembles flous. Il existe plusieurs définitions de l'opérateur ET en logique floue. Parmi les plus utilisés, on a :
- L'opérateur de minimalité : a ET b = min(a, b)
- L'opérateur produit : a ET b = a.b
Par exemple, reprenons la règle d'inférence ci-dessus (Si la vitesse est grande ET la distance au feu est courte ALORS freine fort) en utilisant l'opérateur de minimalité. Si on sait que la vitesse est grande à 80% et que la distance au feu est courte à 20% alors, je vais freiner fort à 20%. Tandis que si j'utilise l'opérateur produit, je freinerai fort à 16%.
Il existe une troisième interprétation de l'opérateur ET logique qui se nome le ET flou. Cet opérateur est un mixe entre l'opérateur de minimalité et la moyenne arithmétique. Le ET flou se défini comme ça :
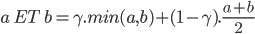
Le ET flou possède un paramètre 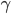 qui est compris entre 0 et 1 et qui doit être fixé par le concepteur du système flou. Si
qui est compris entre 0 et 1 et qui doit être fixé par le concepteur du système flou. Si 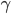 vaut 1, on se retrouve avec l'opérateur de minimalité tel que défini plus haut.
vaut 1, on se retrouve avec l'opérateur de minimalité tel que défini plus haut.
Si on reprend l'exemple ci-dessus, mais en utilisant le ET flou avec un 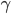 à 0.5 : 80% ET 20% = 0.5 min(80%, 20%) + 0.5 (80% + 20%) /2 = 35%. Je devrais donc freiner fort à 35%.
à 0.5 : 80% ET 20% = 0.5 min(80%, 20%) + 0.5 (80% + 20%) /2 = 35%. Je devrais donc freiner fort à 35%.
L'opérateur OU (S-Norme ou T-Conorme)
Le OU en logique floue correspond à l'union de deux ensembles flous. Comme pour le ET logique, il existe plusieurs définitions du OU logique dans le cadre de la logique flou :
- L'opérateur de maximalité : a OU b = max(a,b)
- L'opérateur produit : a OU b = 1-(1-a).(1-b)
Si nous modifions la règle d'inférence ci-dessus pour avoir un OU dans les conditions : Si la vitesse est grande OU la distance au feu est courte ALORS freine fort
Dans ce cas, si on utilise l'opérateur de maximalité, je freinerais fort à 80%, et avec l'opérateur produit, je freinerais fort à 84%.
De même que pour le ET, il existe un troisième opérateur assez connu pour le OU logique : le OU flou. Cet opérateur est défini comme une combinaison entre l'opérateur maximum et la moyenne arithmétique.
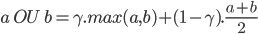
Si l'on choisit le OU flou avec un gamma de 0.5, il faudra donc freiner fort à 65%.
L'opérateur NON
L'opérateur NON en logique flou correspond à l'ensemble complémentaire et est défini simplement : NON a = 1 - a.
Bien sûr, le choix des opérateurs revient entièrement au concepteur du système flou. Celui-ci peut même décider de créer ses propres opérateurs qui remplaceront les opérateurs logiques moyennant de respecter certaines propriétés algébriques (associativité, commutativité, monotonie et, respectivement, 0 comme élément absorbant et 1 comme élément neutre pour un opérateur ET et 1 comme élément absorbant et 0 comme élément neutre pour un opérateur OU).
Une fois que l'on a dressé une liste de règles d'inférences, que l'on a choisi les opérateurs logiques que l'on souhaitait utiliser, il suffit qu'appliquer chaque règles aux variables linguistiques calculés dans l'étape de fuzzification. Les résultats de ces règles pourront directement aller à l'étape finale de défuzzification.
La défuzzification
La dernière étape pour avoir un système flou opérationnel s'appelle la défuzzification. Lors de la seconde étape, on a généré un tas de commandes sous la forme de variables linguistiques (une commande par règle). Le but de la défuzzification est de fusionner ces commandes et de transformer les paramètres résultants en donnée numérique.
L'étape de défuzzification se déroule en deux temps :
D'abord, il faut fusionner les variables linguistiques communes à l'aide d'un opérateur de la logique floue choisi par le concepteur du système. Si on a plusieurs règles d'inférences qui génèrent plusieurs valeurs de la même variable linguistique, on peut choisir un opérateur pour combiner les valeurs de la variable. Cet opérateur sera dans la grande majorité des cas, le OU logique utilisant l'opérateur de maximalité. Par exemple, si on a trois règles qui génèrent la variable linguistique accélère fortement à 20%, 25% et 35%. Il en résultera que la variable accélère fortement aura pour valeur finale 35%.
Dans un second temps, nous pouvons réellement entamer la partie délicate de la défuzzification. On a une série de variables linguistiques qui caractérisent une seule et même donnée. Par exemple, on peut avoir trois variables linguistiques : accélération forte à 35%, accélération moyenne à 80% et accélération faible à 0% qui qualifie l'accélération. Ces variables linguistiques possèdent chacune une fonction d'appartenance. Défuzzifier la donnée d'accélération revient donc à trouver la meilleure valeur quantitative en fonction des fonctions d'appartenances des variables linguistiques.
Il existe plusieurs méthodes pour défuzzifier. Parmi les plus utilisés, on peut citer la méthode de la moyenne des maximas et la méthode du centre de gravité.
La méthode de la moyenne des maximas revient à prendre l'abscisse correspondant à la moyenne des abscisses ayant pour ordonnée la valeur maximale des fonctions d'appartenance. Dans le cas précédent, le maximum de la fonction d'appartenance, c'est 80% pour la variable linguistique accélération moyenne. Il faut donc faire la moyenne des abscisses pour lesquels la fonction d'appartenance accélération moyenne est supérieure ou égal à 80%.
D'un point de vue formel, la méthode de la moyenne des maximas s'exprime de cette façon : 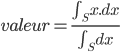 avec
avec 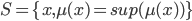
La seconde méthode est la méthode du centre de gravité. Elle consiste à prendre l'abscisse correspondant au centre de gravité de la fonction d'appartenance. Formellement, on l'exprime comme : 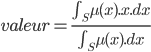 avec S, le domaine de la fonction d'appartenance.
avec S, le domaine de la fonction d'appartenance.
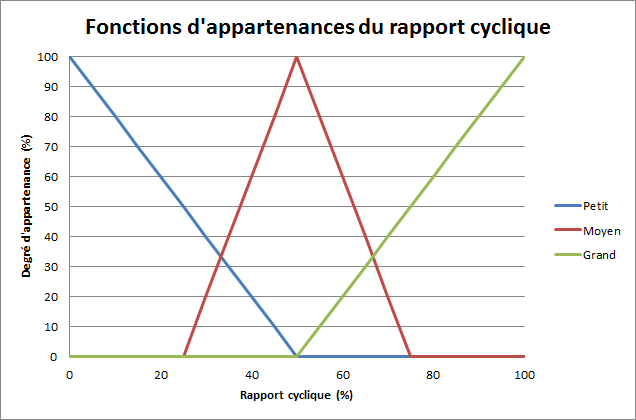
Pour illustrer ces deux méthodes de défuzzification, prenons un exemple. L'on souhaite régler le rapport cyclique d'un moteur à l'aide d'un système flou. On fournit au système des données brutes et un ensemble de règles d'inférence. Le système calcul automatiquement les sorties sous forme de variables linguistiques. On suppose que les variables linguistiques de sorties sont rapport cyclique faible à 0%, rapport cyclique moyen à 80% et rapport cyclique fort à 30%.
L'on considère que l'on a choisi les fonctions d'appartenances suivantes pour chacune des trois variables linguistiques :
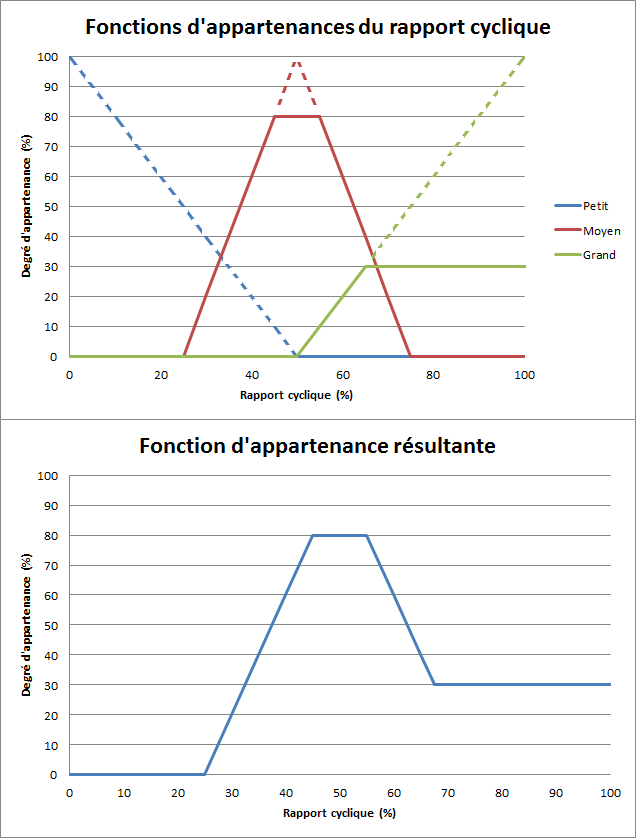
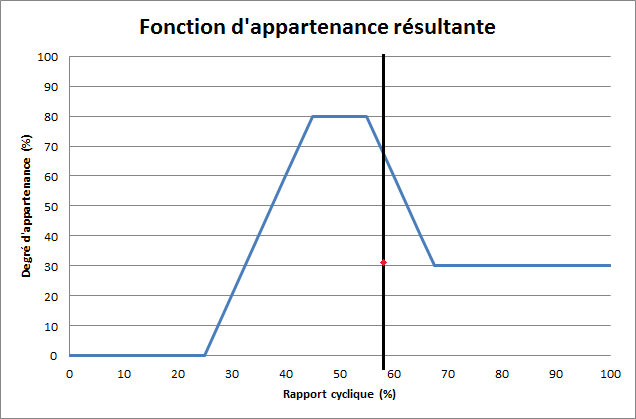
Avec les données en sortie du moteur d'inférence, on est capable de générer la nouvelle fonction d'appartenance :
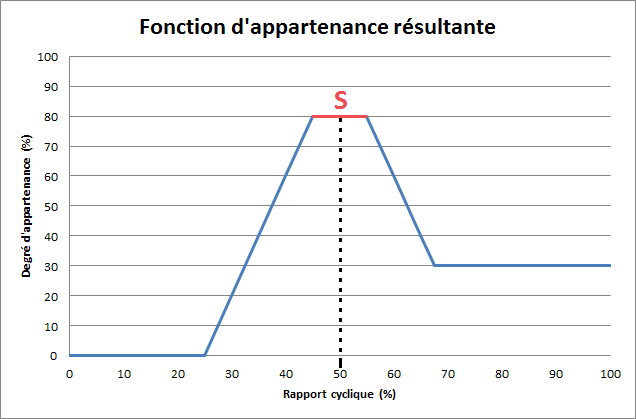
Ainsi, pour défuzzifier, si l'on applique la première méthode de la moyenne des maximas, on remarque que la fonction d'appartenance résultante est maximale pour un rapport cyclique compris entre 40 et 60%. Il suffit de faire la moyenne sur l'intervalle [40,60] pour trouver le rapport cyclique résultant. Ici, le résultat de la défuzzification vaudra 50%.
La seconde méthode du centre de gravité donne des résultats bien meilleurs et est largement utilisée dans les systèmes flous. Néanmoins, elle possède l’inconvénient d'être très couteuse. En effet, pour appliquer cette méthode de défuzzification, il faut calculer le centre de gravité de la surface sous la fonction d'appartenance et de prendre l'abscisse de ce centre de gravité. Pour cela, il faut décomposer la fonction d'appartenance en petits morceaux et intégrer sur chacun des morceaux.
![\left\{ \begin{array}{l r} \mu (x) = \left( x-25 \% \right) .4 & x \in [25 \% ,45 \% ] \\ \mu (x)=80 \% & x \in [45 \% ,55 \% ] \\ \mu (x)=80 \% - \left( x-55 \% \right) .4 & x \in [55 \% , 67.5 \% ] \\\mu (x)=30 \% & x \in [67.5 \% ,100 \% ] \end{array} \right.](http://www.ferdinandpiette.com/blog/wp-content/plugins/latex/cache/tex_cdc75247ab17596a127be6c9c0847df4.gif)
Il suffit maintenant d'appliquer l'intégrale du centre de gravité :

La valeur du rapport cyclique calculée à l'aide de la défuzzification par centre de gravité vaut donc 58%, ce qui est une valeur plus réaliste.
La défuzzification est une partie délicate à implémenter dans un système flou. En effet, elle consomme généralement pas mal de ressource informatique pour pouvoir transformer les variables linguistiques en données numériques, car dans cette partie, on manipule des fonctions. Ceci peut être un point critique dans un système embarqué et le choix de la méthode de défuzzification y est donc crucial.
Exemple de système flou
Pour finir cet article, voici un petit exemple très simple de système flou qui a pour avantage d'avoir une défuzzification assez simple puisque les variables de sorties sont déjà des variables numériques et non linguistiques. Il suffit, pour défuzzifier de fusionner ces variables numériques sans manipuler des fonctions d'appartenances.
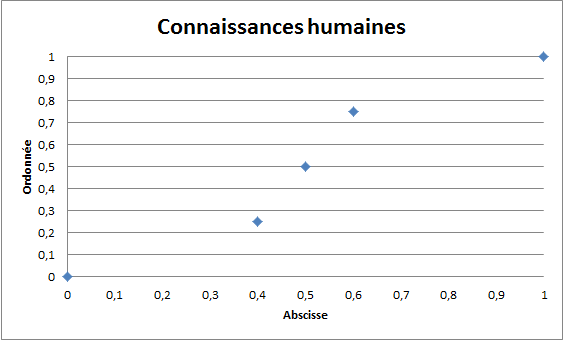
L'exemple en question est un système flou qui a pour but de faire de l'interpolation de points. Les connaissances que l'on a du système sont les coordonnées de cinq points :
- Point 1 : (0, 0)
- Point 2 : (0.4, 0.25)
- Point 3 : (0.5, 0.5)
- Point 4 : (0.6; 0.75)
- Point 5 : (1, 1)
On souhaite donc interpoler un point quelconque dont l'abscisse est comprise entre 0 et 1. En entrée du système, on a l’abscisse d'un point compris entre 0 et 1 et en sortie, on veut l'ordonnée du point interpolé.
Pour cet exemple, nous voulons essayer d'interpoler trois points dont les abscisses sont 0.3, 0.55 et 0.95
Etape 1. La fuzzification
La première chose à faire, c'est de définir les variables linguistiques qui nous seront utiles ainsi que leurs fonctions d'appartenances. Pour cet exemple, je vais choisir cinq variables linguistiques qui caractériseront l'abscisse d'un point. Chacune des variables linguistiques caractérisera un des cinq points que l'on connait.
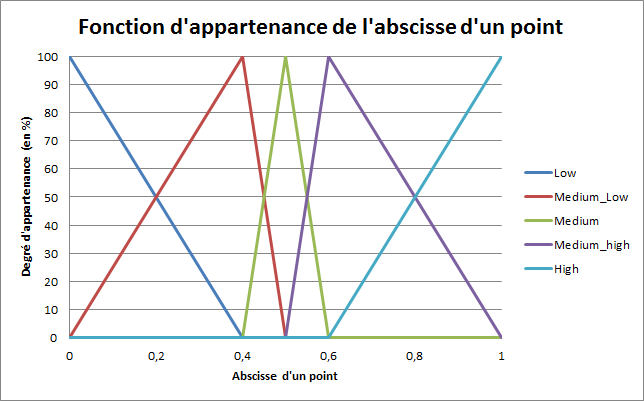
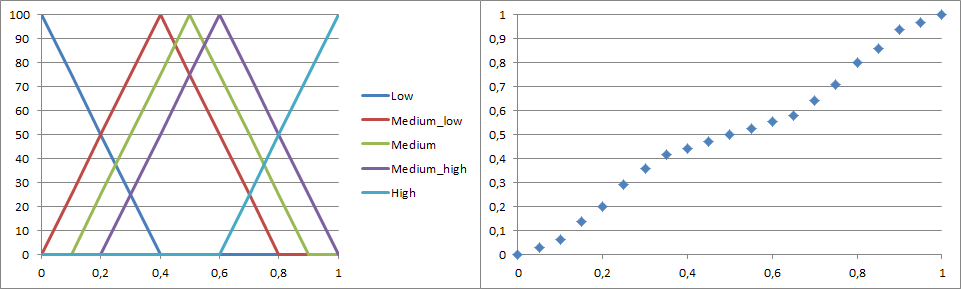
Les variables linguistiques seront nommées ainsi : low, medium_low, medium, medium_high, high. Leurs fonctions d'appartenance seront des fonctions triangles qui seront centrées en chacune des abscisses des points connus. De plus, je choisis que la somme de toutes les fonctions d'appartenances en un point donné donne 1. (Cette propriété n'est pas obligatoire, c'est juste pour simplifier les choses par la suite.)
Voila les cinq fonctions d'appartenances résumés ci-dessous :
Avec ces fonctions d'appartenances, on remarque que chaque point des connaissances est caractérisé à 100% par une seule et unique variable linguistique. (Par exemple, le point 4 est medium_high à 100%)
Nous pouvons maintenant fuzzifier les trois points à interpoler !
- Pour x1 = 0.3, x1 est low à 25% et medium_low à 75%
- Pour x2 = 0.55, x2 est medium à 50% et medium_high à 50%
- Pour x3 = 0.95, x3 est medium_high à 12.5% et high à 87.5%
Etape 2. Le moteur d'inférence
Dans cette partie, on doit tout d'abord définir un ensemble de règles d'inférences dérivé des connaissances humaines. Ici, les règles d'inférences sont plutôt simples. Elles sont au nombre de cinq :
- Si x est low, alors y = 0
- Si x est medium_low, alors y = 0.25
- Si x est medium, alors y = 0.50
- Si x est medium_high, alors y = 0.75
- Si x est high, alors y = 1
On se rend compte que dans notre cas, la sortie n'est pas vraiment à 100% une variable linguistique, car elle comporte déjà une valeur. C'est cette astuce qui va nous soulager des calculs complexes de la défuzzification.
Si on passe les trois points à interpoler dans le moteur d'inférence, on a :
- Pour x1 = 0.3 : y1 = 0 à 25% et y1 = 0.25 à 75%
- Pour x2 = 0.55 : y2 = 0.5 à 50% et y2 = 0.75 à 50%
- Pour x3 = 0.95 : y3 = 0.75 à 12.5% et y3 = 1 à 87.5%
Etape 3. La défuzzification
Vient enfin la dernière étape de défuzzification. Pour cette étape, pas besoin de calculs complexes ! Il suffit de faire la moyenne pondérée des sorties et comme la somme des valeurs des fonctions d'appartenance vaut 1 (25%+75%, 50%+50% et 12.5%+87.5%), pas besoin de diviser par 1 🙂
- Pour x1 = 0.3 : y1 = 0 * 25% + 0.25 * 75% = 0.188
- Pour x2 = 0.55 : y2 = 0.5 * 50% + 0.75 * 50% = 0.625
- Pour x3 = 0.95 : y3 = 0.75 * 12.5% + 1 * 87.5% = 0.969
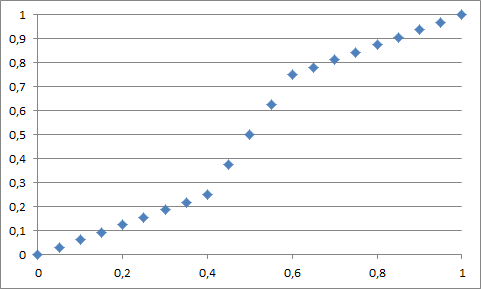
On obtient donc l'interpolation de nos trois points grâce à un système flou :
- (0.3, 0.19)
- (0.55, 0.63)
- (0.95, 0.97)
On peut ainsi interpoler n'importe quelle point d'abscisse comprise entre 0 et 1.
Dans notre cas, on remarque que l'interpolation est linéaire entre deux points "connaissances". Pour rendre l'interpolation non linéaire, il suffit de redéfinir les fonctions d'appartenances afin que la somme des fonctions ne fassent plus forcement 1.
En conclusion, pour réaliser un système flou, il faut dans un premier temps modéliser les données d'entrées en variables linguistiques grâce à des fonctions d'appartenances, dans un second temps, dresser une liste de règles d'inférences qui représentent les connaissances que l'on a du système et enfin, il faut choisir quels sont les opérateurs logiques à utiliser et quel type de defuzzification on souhaite utiliser.
Un système flou est entièrement customisable. Ses performances seront à l'image des réglages que le concepteurs du système à bien voulu faire. Un système flou peut être très performant comme totalement inutile ! (Par exemple, mon dernier exemple d'interpolation non linéaire n'est pas du tout performant car elle déforme les valeurs connaissances ! Ainsi, l'interpolation de x=0.4 ne fait plus du tout 0.25 :s )
A vous de jouer 😉

Merci infiniment pour vos efforts !
Bonne continuation et surtout ne lâchez pas .
Chapeau pour vous .
Très bonne explication, merci ! 🙂
Merci pour cet excellent article.
mrcc bcp excellente explication ca ma bcp aidé et bonne continuation
Très bonne explication
Merci infiniment continuer.