Voici un petit article rédigé suite à une piqûre de rappel de mes cours d'algèbre de prépa. Ce qui suit n'est pas un cours d'algèbre, loin de là, c'est juste un résumé succinnt des divers propriétés de certaines structures algébriques importantes.
Après une brève introduction sur la théorie des ensembles, je rappellerais les propriétés des structures algébriques :
- du groupes, corps, anneaux
- du K-espace vectoriel et du A-modules,
- de l'espaces euclidien, hermitien et pré-hilbertien
- de l'algèbres sur un anneau et sur un corps
En plus de ses structure, j'ai rédigé un petit rappel de certaines définitions importantes comme :
- les applications linéaires
- les formes bilinéaire
- les produits scalaire
I. Les ensembles : la base de l'algèbre
L'algèbre se base sur la théorie des ensembles qui est une théorie fondamentale conçu par Cantor au XIXème siècle. Un ensemble est une notion première qui désigne de façon intuitive une collection d'objets. Les objets, ou éléments d'un ensemble peuvent être de types différents. On peut avoir un ensemble de points, un ensemble de nombres, un ensemble de jours ou encore un ensemble de fruits. Ce qui est essentiel dans la théorie des ensembles initialement développée, c'est la notion d'appartenance, c'est-à-dire le fait de savoir si un objet fait partie d'un ensemble ou non.
Bien souvent, on représente un ensemble par une lettre majuscule (E, A, etc.) et un élément d'un ensemble par une lettre minuscule (x, y, etc.). L'appartenance d'un élément x à un ensemble A se note 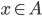 et se lit x appartient à A.
et se lit x appartient à A.
A contrario, pour désigner la non-appartenance, on utilise le symbole 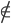 qui signifie n'appartient pas à.
qui signifie n'appartient pas à.
A partir de cette relation d'appartenance et des opérateurs issus de la logique classique, la théorie des ensembles définie plusieurs opérateurs permettant de manipuler ces ensembles.
L'égalité
Deux ensembles sont dit égaux si et seulement si tous les éléments du premier ensemble appartiennent aussi au second ensemble et inversement.
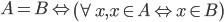
L'union
L'union de deux ensembles A et B est l'ensemble C comportant tous les éléments appartenant à A ou à B. On note alors 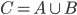 : l'ensemble C est l'union des ensembles A et B.
: l'ensemble C est l'union des ensembles A et B.
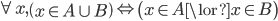
L'intersection
L'intersection de deux ensembles A et B est l'ensemble C comportant les éléments appartenant à la fois à A et à B. On note ainsi 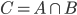 : l'ensemble C est l'intersection des ensembles A et B.
: l'ensemble C est l'intersection des ensembles A et B.
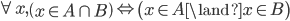
L'inclusion
On dit que A est inclut dans B ou encore, que A est un sous-ensemble de B (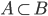 ) si l'intersection de A est de B est égal à A.
) si l'intersection de A est de B est égal à A.
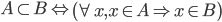
Le produit cartésien
Le produit cartésien C de deux ensembles A et B est l'ensemble des couples dont la première composante appartient à A et dont la seconde appartient à B. On le note 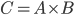
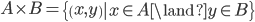
Ceci n'est pas une liste exhaustive de tous les opérateurs sur les ensembles, seulement quelques uns des plus importants. Il en existe beaucoup d'autres comme l'ensemble des parties, la somme disjointe, le cardinal, l'exponentiation, etc.
II. Les structures algébriques
Les structures algébriques sont l'association d'un ou plusieurs ensembles avec une ou plusieurs lois de composition respectant divers propriétés. Une loi de composition est une application qui peut être de deux types :
- Soit une application de
 dans
dans 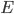 . On dit que la loi de composition est interne.
. On dit que la loi de composition est interne. - Soit une application de
 dans
dans 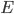 ou de
ou de 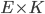 dans
dans 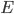 . On dit que la loi de composition est externe respectivement à gauche et à droite.
. On dit que la loi de composition est externe respectivement à gauche et à droite.
1. La structure de base : Le groupe
Le groupe (E,+)
On appelle groupe, le couple 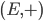 : l'ensemble E muni d'une loi de composition interne notée
: l'ensemble E muni d'une loi de composition interne notée 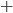 , appelé addition qui respecte trois propriétés :
, appelé addition qui respecte trois propriétés :
- L'associativité :
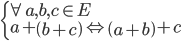
- L'élément neutre : e est appelé élément neutre du groupe
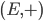
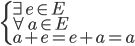
- La symétrie : Où e est l'élément neutre du groupe
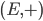 . On dit alors que b est l'élément symétrique de a.
. On dit alors que b est l'élément symétrique de a.
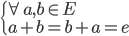
Le groupe abélien (E,+)
Un groupe est dit abélien (ou commutatif) s'il respecte une quatrième propriété :
- La commutativité :
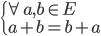
Par exemple, le couple 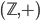 possède une structure de groupe abélien avec 0 pour élément neutre.
possède une structure de groupe abélien avec 0 pour élément neutre.
De même, 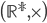 est un groupe commutatif avec 1 comme élément neutre.
est un groupe commutatif avec 1 comme élément neutre.
2. L'anneau et le corps
Les anneaux (E,+,x)
Une structure d'anneau est un triplet contenant un ensemble et deux lois de composition internes 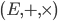 respectant plusieurs propriétés :
respectant plusieurs propriétés :
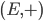 possède une structure de groupe commutatif
possède une structure de groupe commutatif- La multiplication (seconde loi de composition interne) est associative :
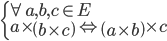
- La multiplication est distributive sur l'addition :

- Il existe un élément neutre pour la multiplication noté 1 :
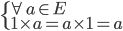
Les corps (E,+,x)
Un corps, tout comme l'anneau, est un triplet contenant un ensemble et deux lois de composition internes 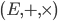
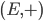 possède une structure de groupe commutatif
possède une structure de groupe commutatif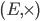 possède une structure de groupe
possède une structure de groupe- La multiplication est distributive sur l'addition :

Un corps est dit commutatif si 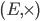 est un groupe abélien.
est un groupe abélien.
3. L'espace vectoriel
L'espace vectoriel (E,K,+,.)
Un espace vectoriel E sur un corps K possède :
- une loi de composition interne de
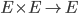 noté
noté 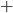 et appelé addition vectorielle
et appelé addition vectorielle - une loi de composition externe à gauche de
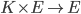 noté
noté  et appelé multiplication par un scalaire
et appelé multiplication par un scalaire
Un élément de E est appelé un vecteur alors qu'un élément du corps K est appelé un scalaire.
Pour que E soit un K-espace vectoriel (un espace vectoriel sur le corps K), il doit respecter les propriétés suivantes :
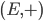 possède une structure de groupe abélien
possède une structure de groupe abélien- La loi externe de multiplication par un scalaire de E est distributive à gauche par rapport à la loi interne de somme vectorielle de E :
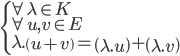
- La loi externe de multiplication par un scalaire de E est distributive à droite par rapport à la loi interne l'addition du corps K :
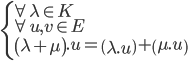
- La loi externe de multiplication par un scalaire de E est associative à droite par rapport à la loi interne multiplication du corps K :
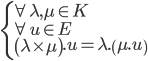
- L'élément neutre de la loi interne multiplication du corps K est aussi élément neutre à gauche pour la loi externe de multiplication par un scalaire de E :
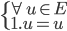
Remarque : la loi de composition interne 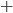 de l'espace vectoriel et du corps se note de la même manière par abus de langage bien que ce soit deux opérateurs différents.
de l'espace vectoriel et du corps se note de la même manière par abus de langage bien que ce soit deux opérateurs différents.
Le module (E,A,+,.)
Un module est un espace vectoriel auquel on a remplacé le corps par un anneau. Toutes les propriétés de l'espace vectoriel sont respectés. La seule différence est que le corps K de l'espace vectoriel est un anneau A dans le cas d'un module.
4. Les espaces pré-hilbertiens
Définition de l'application linéaire
Une application linéaire f (ou morphisme d'espace vectoriel) est une application entre deux espaces vectoriels (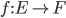 ) qui respecte les combinaisons linéaires. Autrement dit, c'est une application respectant les deux propriétés suivantes :
) qui respecte les combinaisons linéaires. Autrement dit, c'est une application respectant les deux propriétés suivantes :
- L'additivité (respect de l'addition des vecteurs) :
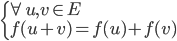
- L'homogénéité (respect de la multiplication par un scalaire) :
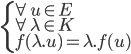
Une application est additive et homogène (une application est dite linéaire) si et seulement si :
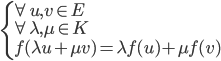
Une application linéaire est dite un endomorphisme d'espace vectoriel si l'espace vectoriel de départ est le même que l'espace vectoriel d'arrivé : 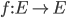
Une application linéaire est dite un isomorphisme d'espace vectoriel si l'application est bijective.
Une application linéaire est dite un automorphisme d'espace vectoriel si c'est à la fois un endomorphisme et un isomorphisme.
Définition de la forme bilinéaire
Une forme est une application d'un espace vectoriel E dans son corps K.
Soit E et F, deux espaces vectoriels sur K (ou K-espace vectoriel). Une forme bilinéaire est une application de 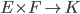 qui respecte la linéarité de l'élément de E vis-à-vis de l'élément de F et inversement.
qui respecte la linéarité de l'élément de E vis-à-vis de l'élément de F et inversement.
Une forme est dite bilinéaire si :

Définition du produit scalaire
Un produit scalaire est une application bilinéaire symétrique définie positive de 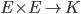 .
.
- Une forme bilinéaire
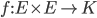 est dit symétrique si :
est dit symétrique si :
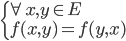
- Une forme bilinéaire est définie si :
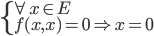
- Une forme bilinéaire est positive si :
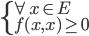
Les espaces euclidiens
Un espace vectoriel euclidien est un espace vectoriel E fini sur le corps des réels muni d'un produit scalaire.
Les espaces hermitiens
Un espace vectoriel hermitien est un espace vectoriel E fini sur le corps des complexes muni d'un produit scalaire.
Les espaces pré-hilbertiens
Un espace vectoriel pré-hilbertiens est un espace vectoriel E fini ou infini sur le corps des complexes muni d'un produit scalaire.
5. Les algèbres
Les algèbres sur aneaux (E,A,+,.,x)
Une algèbre sur un anneau possède :
- Un module
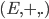 sur un anneau commutatif A
sur un anneau commutatif A - Une loi de composition interne bilinéaire
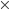 de
de 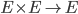 que l'on appellera multiplication vectorielle. Cette loi, pour être bilinéaire, doit respecter les propriétés suivantes :
que l'on appellera multiplication vectorielle. Cette loi, pour être bilinéaire, doit respecter les propriétés suivantes :
- Distributive par rapport à la somme vectorielle :

-
- Compatible avec la multiplication par un scalaire :
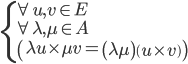
Les algèbres sur corps (E,K,+,.,x)
Une algèbre sur un corps possède :
- Un espace vectoriel
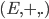 sur un corps K
sur un corps K - Une loi de composition interne bilinéaire
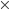 de
de 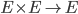
Remarque, un produit scalaire est une multiplication vectorielle munie de la propriété d'anti-symétrie :
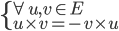
III. Résumé
Groupe E
- Addition : Loi de composition interne
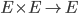
Anneau, Corps E
- Addition : Loi de composition interne
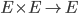
- Multiplication : Loi de composition interne
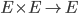
K-Espace Vectoriel E
- Somme vectoriel : loi de composition interne
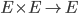
- Multiplication par un scalaire : loi de composition externe à gauche
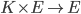
Espace pré-hilbertien
- Somme vectoriel : loi de composition interne
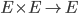
- Multiplication par un scalaire : loi de composition externe
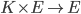
- Produit scalaire : application bilinéaire
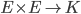
Algèbre
- Somme vectoriel : loi de composition interne
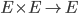
- Multiplication par un scalaire : loi de composition externe
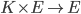
- Multiplication vectorielle : loi de composition interne bilinéaire
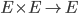

Deux petites corrections:
- dans ta définition de corps, il faut demander que E privé de 0 soit un groupe pour la multiplication (sinon, comme 0 est absorbant, le seul "corps" ainsi défini serait réduit au nul);
- la définition de produit scalaire que tu donnes est celle utilisée pour les espaces vectoriels réels; il faut l'adapter un peu pour les espaces complexes.
🙂
Oh, merci Gabriel pour les corrections !
En effet, j'ai donné la définition d'un produit scalaire dans un espace réel. Pour les complexes, il faudrait donc que je définisse la symétrie hermitienne (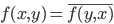 ) et la propriété de sesquilinéarité (linéaire d'un côté et semilinéaire de l'autre)...
) et la propriété de sesquilinéarité (linéaire d'un côté et semilinéaire de l'autre)...
Je corrige ça dès que possible !
Ferdi
Bonjour, merci pour ce très bon résumé qui me fait gagner beaucoup de temps !
J'ai juste remarqué une petite erreur dans la definition d'un groupe pour la propriété de symétrie :
Il est dit "pour tout a,b a+b=b+a=e"
Ca serait pas "pour a il existe b" ?
Merci