Dans cet article, vous trouverez une brève introduction au filtre de Kalman. J'essayerai de vous expliquer progressivement comment ce filtre est apparu. Cet article demande au lecteur d'avoir certaines bases en mathématiques, notamment en calcul matriciel et sur les variables aléatoires et les probabilités. Enfin, si vous avez déjà saisi le principe de cet estimateur, vous arriverez à lire cet article sans problème.
Je vais donc commencer par faire quelques rappels sur les estimateurs déterministes, présenter l'estimateur des moindres carrés. Ensuite, je complexifierai le modèle progressivement jusqu'à obtenir un filtre de Kalman.
Prérequis : Si vous n'avez aucune idée de ce qu'est le filtre de Kalman, il vaudrait peut-être mieux commencer par cet article pour en comprendre le principe : Le filtre de Kalman : intérêts et limites
I. L'estimation
L'estimation est une branche des mathématiques statistiques qui permet, à partir de mesures effectuées sur un système, d'estimer la valeur de différents paramètres de ce système.
Vous manipulez des estimateurs tous les jours et ce, peut-être sans même vous en rendre compte. Par exemple, sur les bancs de l'école, pour estimer votre niveau scolaire, vous faites la moyenne de vos notes obtenues lors des contrôles. Les notes correspondent donc aux différentes mesures effectuées, votre niveau scolaire est le paramètre à estimer (il est inaccessible. Vous ne pouvez pas le connaitre, mais vous pouvez l'estimer) et enfin, la moyenne est votre estimateur.
Bien sûr, il est possible de n'estimer qu'un seul paramètre (votre niveau scolaire par exemple), mais il vous est aussi possible d'estimer plusieurs paramètres en même temps. Dans ce cas, on ne parle plus de paramètre à estimer, mais de vecteur à estimer, ou vecteur d'état.
II. Les Estimateurs déterministes
Tout d'abord, un point important dans la philosophie des estimateurs déterministes est que le vecteur à estimer est justement déterministe. C'est-à-dire que l'on suppose que ce vecteur possède des valeurs non aléatoires, même si celles-ci sont inaccessibles. Ce que l'on cherche à trouver, c'est un estimateur qui estime au mieux ce vecteur.
Pour ça, il faut que l'estimateur soit sans biais et de variance minimale (pour minimiser l'erreur d'estimation).
-
Le biais
Un estimateur sans biais signifie que l'espérance de l'estimation doit être égale au vecteur à estimer. En gros, ça veut donc dire que l'estimateur, en moyenne, ne commet pas d'erreur. Dit encore autrement, si l'on fait la moyenne des estimations, on trouve la valeur réelle du paramètre. Bien sûr, le biais n'est pas calculable en réalité, car on ignore la valeur réelle du paramètre ou du vecteur à estimer. Par contre, il est très utile pour caractériser nos estimateurs.
-
La variance
La variance peut être assimilée à l'erreur. Un estimateur est dit à variance minimal lorsque l'on a réussi à minimiser les variations entre le vecteur d'état et l'estimation. On a donc minimisé l'erreur.
Il faut bien faire attention, car ces deux notions sont bien distincte. Un estimateur peut très bien avoir un biais nul, mais si sa variance est forte, cet estimateur ne sera pas performant.
-
Exemple
Pour cet exemple, nous allons qualifier en termes de biais et de variance différents estimateurs. Le paramètre à estimer sera une tension constante de 230 volts.
Tout d'abord, commençons par un estimateur sans biais, mais à forte variance. Les valeurs estimées pourraient être les suivantes : 200, 260, 300, 220, 240, 160. Vous remarquerez que la moyenne fait bien 230. Donc notre estimateur est bien sans biais. Par contre, la variance est gigantesque. Notre estimateur n'est donc pas performant.
Voyons maintenant ce que donnerait un estimateur à faible variance, mais avec un biais de 11 par exemple. Les estimations fournies par cet estimateur pourrait être : 240, 241, 242, 241, 241, 242, 240. Ici, les valeurs sont très rapprochées. La variance est donc très faible, par contre, on constate une erreur de 11 volts entre la valeur moyenne de l'estimation et la valeur du paramètre. Le biais fausse donc le résultat.
Enfin, voici un exemple d'estimation que l'on pourrait obtenir avec un estimateur sans biais et à variance minimale : 229, 230, 231, 231, 230, 230, 229. Ici, la moyenne fait 230, donc le biais est bien nul. Et la variance est très faible car toutes les valeurs sont comprises dans une bande de 2 volts de large.
Cet exemple illustre donc l'intérêt d'avoir un estimateur avec un biais nul et une variance très faible.
III. L'estimateur optimal
Dans la littérature, vous trouverez qu'un estimateur dont le biais est nul aura une variance toujours supérieur ou égale à ce que l'on appelle la "borne de Cramer-Rao". Finalement, c'est assez logique. On ne peut pas obtenir une variance nulle et donc, on ne peut pas connaitre exactement la valeur du vecteur d'état. On aura toujours une incertitude égale à la borne de Cramer-Rao pour l'estimateur optimal. Si la variance est nulle, alors ce n'est plus un problème d'estimation, car ça voudrait dire que l'on connait la valeur à estimer dès le départ.
Il se trouve que dans certains cas particuliers, il existe un estimateur sans biais à variance minimale calculable. Mais pour cela, il faut que le système respecte quelques contraintes :
- Le bruit doit être Gaussien
- Le système doit être linéaire
Cet estimateur est appelé "Estimateur sans biais à variance minimale linéaire gaussien", ou encore "Estimateur optimal linéaire gaussien" ou tout simplement "Méthode des moindres carrés".
IV. La méthode des moindres carrés
La première chose pour trouver cet estimateur est de modéliser le système de façon linéaire grâce à une équation d'état de ce type :
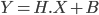
Avec :
- Y, le vecteur de mesure (obtenue grâce aux capteurs)
- X, le vecteur des paramètres à estimer
- B, la vecteur du bruit de mesure (bruit gaussien engendré par les capteurs)
- H, la matrice reliant l'état à la mesure (appelé matrice d'observation)
Il faut donc avant toute chose déterminer ces quatre matrices. Les matrices Y et B sont déterminés très facilement. En effet, ce sont les informations obtenues grâce aux capteurs ainsi que les bruits des différents capteurs. Le vecteur X est le vecteur des paramètres que vous voulez estimer. Enfin, la matrice H est à déterminer pour pouvoir respecter l'égalité.
Une fois le modèle posé, on peut donc calculer l'estimateur optimal.
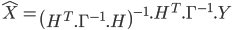
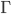 est la matrice de covariance du bruit de mesure. Pour un bruit gaussien centré avec des capteurs décorrélés entre eux, cette matrice est diagonale et ses termes sont les écart-types des différents bruits gaussien des capteurs.
est la matrice de covariance du bruit de mesure. Pour un bruit gaussien centré avec des capteurs décorrélés entre eux, cette matrice est diagonale et ses termes sont les écart-types des différents bruits gaussien des capteurs.
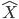 est l'estimation de X.
est l'estimation de X.
La variance de cet estimateur est la borne de Cramer-Rao : 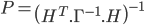
Voilà, nous avons notre estimateur optimal linéaire gaussien. Maintenant, imaginons que l'on ai k mesures indépendantes. Nous pouvons donc faire une estimation de notre vecteur d'état grâce à cet estimateur. Mais une fois notre estimation calculée, si une autre mesure nous arrive, il faudra redéfinir toutes les matrices et recommencer les calculs pour obtenir une nouvelle estimation.
En réalité, ce genre de choses est infaisable, notamment lorsque l'on doit traiter un problème en temps réel (en effet, les matrices seront de plus en plus grandes et il y a des inversions matricielles à faire, ce qui prend énormément de temps).
Heureusement, il existe une expression récursive de cette estimateur, que nous allons voir tout de suite.
V. La méthode des moindres carrés récursive
Avec k mesures, notre estimateur optimal s'écrit donc comme cela :
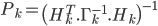
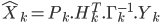
Pour k+1 mesures, l'estimateur devient :
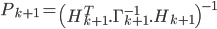
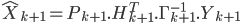
Ce que l'on cherche à faire, c'est d'écrire 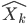 en fonction de
en fonction de 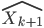 .
.
On arrive donc à l'expression récursive :
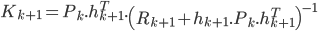
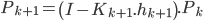
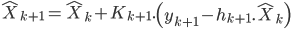
Ici, les notations ont un peu changé :
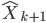 , la prédiction à l'état k+1 (ça n'a pas changé)
, la prédiction à l'état k+1 (ça n'a pas changé)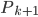 , la covariance de l'erreur à l'instant k+1 (ça n'a pas changé)
, la covariance de l'erreur à l'instant k+1 (ça n'a pas changé)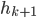 , la matrice d'état non pas pour les k+1 mesures (matrice H), mais uniquement pour la mesure courante. (Dans le cas des moindres carrés ou de Kalman,
, la matrice d'état non pas pour les k+1 mesures (matrice H), mais uniquement pour la mesure courante. (Dans le cas des moindres carrés ou de Kalman, 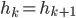 )
)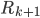 , la matrice de covariance du bruit de mesure, non plus pour k+1 mesures (matrice
, la matrice de covariance du bruit de mesure, non plus pour k+1 mesures (matrice 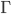 ), mais pour une seule mesure uniquement. (Pour le filtre de Kalman, on a aussi
), mais pour une seule mesure uniquement. (Pour le filtre de Kalman, on a aussi 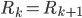 )
)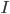 , la matrice identité
, la matrice identité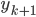 , la mesure à l'instant k+1
, la mesure à l'instant k+1
Pour alléger l'écriture, l'équation a été décomposée en trois parties, faisant apparaitre 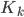 , le gain de Kalman. Ces équations ont déjà une structure très proche d'un Kalman classique.
, le gain de Kalman. Ces équations ont déjà une structure très proche d'un Kalman classique.
VI. Évolution des paramètres dans le temps
Précédemment, le vecteur d'état à estimer était constant. Maintenant, on suppose qu'il évolue dans le temps.
Dans cette partie, on suppose que ce vecteur évolue selon un processus linéaire déterministe supposé connu. On est donc obligé de faire une prédiction de l'estimation courante ( 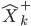 ) à partir de l'estimation précédente (
) à partir de l'estimation précédente ( 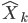 ) suivant le processus linéaire avant d'appliquer les formules de la méthode des moindres carrés récursives, vue précédemment pour calculer l'estimation suivante (
) suivant le processus linéaire avant d'appliquer les formules de la méthode des moindres carrés récursives, vue précédemment pour calculer l'estimation suivante ( 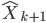 ).
).
On a donc 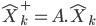
La matrice A relis l'état précédent à l'état suivant. Pour déterminer cette matrice, posez les équations reliant les deux états, puis déterminer la forme matricielle.
De même, il faut prédire la matrice de covariance de l'erreur ( 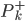 ) :
) : 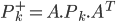
Maintenant que l'on a nos prédictions, il faut mettre à jour afin de prendre en compte la nouvelle mesure effectuée. On peut donc appliquer notre méthode des moindres carrés récursive et ainsi prendre en compte la nouvelle mesure :
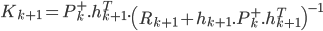
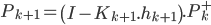
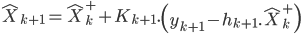
Ceci est presque la forme finale du filtre de Kalman. Nous avons bien la phase de prédiction (les deux premières équations) et la phase de mise à jour (les trois suivantes).
VII. Évolution aléatoire dans le temps
Pour finir, le vecteur à estimer évolue selon un processus linéaire, mais cette fois-ci aléatoire. Il suffit donc de rajouter un bruit d'état lors de la prédiction de la covariance de l'erreur. Ce qui signifie que l'on connait la forme de l'évolution, mais que l'on autorise au système de se tromper.
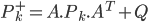
Q est la matrice de covariance du bruit d'état.
Nous avons fini par retomber sur la forme finale du filtre de Kalman.
La phase de prédiction
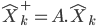
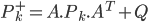
La phase de mise à jour
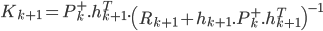
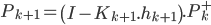
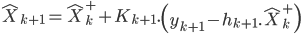
VII. Conclusion
A partir de l'estimateur optimal linéaire gaussien, qui est l'estimateur sans biais atteignant la borne de Cramer-Rao, nous avons trouvé sa forme récursive et nous l'avons adapté afin qu'il puisse estimer un vecteur d'état variant dans le temps. Nous sommes donc arrivé à écrire un filtre de Kalman. Ce filtre nous assure donc que l'estimateur converge vers l'estimateur optimal.
Il est intéressant de préciser que ce filtre nécessite une étape d'initialisation afin de déterminer la première estimation du vecteur d'état ainsi que la matrice de covariance de l'erreur. Ces matrices, si l'on ne connait pas les conditions initiales du système, peuvent être obtenues soit par une méthode ad-hoc (on fixe le vecteur d'estimation plus ou moins au pif et l'on attribue une erreur importante à cette estimation), soit on utilise un autre estimateur, par exemple, la méthode des moindres carrés classique afin d'initialiser le filtre.
Le filtre de Kalman est donc une méthode d'estimation très puissante. Mais elle possède plusieurs faiblesses. Tout d'abord, le modèle doit être linéaire. Heureusement, il existe une variante de ce filtre, appelé le filtre de Kalman étendu qui permet de résoudre des problèmes non linéaire, bien que la stabilité de l'estimateur ne soit plus assurée. Une autre méthode qui, dans certains cas, est plus puissante que le filtre de Kalman est le filtre particulaire.
Si vous voulez un exemple d'utilisation du filtre de Kalman, n'hésitez pas à lire cet article : Exemple d'utilisation du filtre de Kalman

Merci pour ces explications claires et concrètes sur le filtre de Kalman. La plupart des articles du net ne détaillent que la partie mathématiques ou restent flous quant à l'application de cette méthode d'estimation.
Merci pour vos encouragements. Si vous avez le moindre problème concernant les articles, n'hésitez pas à m'en faire part afin que je puisse mieux cibler les passages obscurs !
Est ce qu'on peut comparer les matrices de covariances Pkk entre elles
Bonjour,
On peut en effet comparer les matrices de covariances Pk entre-elles. D'ailleurs, en traçant un graphique des Pk en fonction du temps, on s’aperçoit que la covariance de l'erreur converge vers la borne de Cramer-Rao qui est l'erreur minimale atteignable en estimation.
Salut
merci de vos écrit assez édifiant.
est il possible d'avoir un lien sur la simulation du filtre de Kalman sous Matlab
merci
bonjour, je vous remercie pour cet article mai j'aimerais savoir la nature des matrices utilisés pour ce filtre (est ce qu'ils sont symétrique, diagonal, semi défni positif,.....) merci en avance
Bonjour. Les matrices utilisés sont A, P, Q, H et R :
- A et H sont respectivement les matrices de transitions et d'observation du système. Ces matrices sont déterminées par le concepteur du filtre de Kalman une fois la modélisation du système faite. Elles peuvent donc prendre n'importe quelle forme.
- Les matrices Q et R sont les matrices de covariance du bruit de commande et du bruit de mesure. Ici, vu qu'on est dans un filtre de Kalman et qu'on considère les bruits comme Gaussiens, on aura des matrices diagonales.
- Enfin P est la matrice de covariance de l'erreur. Les termes les plus importants sont sur la diagonale et en général cette matrice est symétrique (je ne suis jamais tombé sur des matrices non symétriques, mais il faudrait tout de même vérifier cette affirmation)
Je vous félicite pour ce travail et vos explications claires.
J'ai aimé l'exemple de l'estimation du niveau scolaire, ça résume tout en quelque mots
Salut,
Merci de ce très joli travail.
C'est très clair, c'est bien écrit, vraiment merci pour tout çà!!
J'ai juste une question: je pense avoir compris l'intérêt des matrices de covariances du filtre de Kalman qui si je ne me trompe pas, sont l'essentiel du rôle de ce filtre. Le but étant d'estimer l'état du système de la meilleure façon possible en considérant le jeu d'erreurs considérées.
Mais je ne comprends pas vraiment comment agissent ces matrices pour ce faire.
Merci de ton aide.
a bientot
Quentin
Bonjour,
Bonne question. Estimer les matrices de covariances du bruit de commandes et de mesures sont un des points critiques du filtre de Kalman.
Je n'ai pas de méthodes formelles à proposer. Il faut dans la majorité des cas y aller par essais/erreurs jusqu'à avoir un bon compromis performance/adaptabilité.
Néanmoins, il est possible d'avoir une première approximation des composantes des matrices.
- Pour la matrice de covariance du bruit de commande (Q), les valeurs sur la diagonale représentent la covariance de l'erreur maximale autorisé pour chacun des composantes du vecteur d'état.
Il suffit donc de déterminer l'erreur maximale que l'on s'autorise sur la modélisation et de calculer sa variance.
- Pour la matrice de covariance de mesures (R), c'est plus facile. Les termes de la diagonales correspondent à la variance (carré de l'écart type) du bruit des capteurs. L'écart-type est donnée ou se calcule facilement à partir de la datasheet des capteurs. Si tu n'as pas de datasheet, il suffit de faire une série de mesures avec ton capteur afin d'obtenir une belle gaussienne et ainsi pouvoir calculer cet écart-type.
Voila,
J'espère avoir répondu à ta question,
Ferdi
Bonjour, Tout d'abord Merci pour cet effort, en effet je voulais savoir la différence entre le filtre de Kalman ou en calcule le gain K par la résolution de L’équation de Riccati?
Puisque je sais pas la différence entre ces deux puisque les deux minimisent la variance de bruit de L'état et celui de sortie.
Bonjour, je ne connais pas l'équation de Riccati, mais apparemment, il n'y a aucun rapport.
L'équation de Riccati est une équation différentielle normale. Je ne vous pas le lien avec la variance d'un bruit quelconque...
Bonjour, je parle de celui qui minimise le bruit d'état et celui de sortie par la résolution de L’équation algébrique de Riccati (pas différentielle) et en Utilise sous Matlab la fonction Lqe, pour résoudre ce problème est trouver le gain L, dans Le cas d'un bruit stationnaire.
Je vous pose cette question puisque à chaque fois je trouve ce genre de problème, je parle bien sûre de filtre qu'en utilise en automatique pas celui du signal.
Hum, je n'en ai malheureusement aucune idée, c'est hors de mes compétences.
Je vous remercie pour cet article,
J'ai un projet d'estimation de la vitesse du moteur asynchrone par filtre de kalman sous matlab simulink...S'il vous plait vous n'auriez pas déja réalisé un travail du genre par ce que je suis un peux perdue
Au plaisir de vous lire
Non, je n'ai jamais fait ce genre de chose.
Mais le première étape, c'est de trouver ce que vous voulez estimer, ainsi que ce que vous pouvez mesurer.
Ensuite, il faut essayer de relier ces deux vecteurs.
Si L'observateur de kalman sous matlab/simulink que tu cherche , je peux t'aider.
à toi de voir ce que tu cherche en juste, puisque le filtre de kalman récursif tant que il est démontré par fred, je crois qu’il est bcp adapté au traitement de signal (dépistage radar,.......)
Oui cher ami fred, le filtre qu'en cherche en tant que automat-tien, c'est L'observateur de Kalman, tu vois c'est abuse de notation et sur ce lien vous pouvez voir la différence: http://www.escalejeunes.fr/balimbatchad/femtoMicky//enseignementFile/TP_master1_csm.pdf, et je crois c'est la même chose qu'elle cherche L'autre Fille "Amel".
Et j'aime Bcp si vous pouvez dire quelque chose et merci .
Bonjour, je vous remercie pour cet article. En effet, en lisant votre article j'ai pu comprendre "un peu" ce qui se passe dans ce filtre. En fait, je suis un étudiant en 2 éme année Classes prépas, et j'aimerais bien savoir comment est-ce qu'on démontre tous ces résultats si c'est possible 🙂 ?
Bonjour,
Pour démontrer tout ça, il faut, en plus du programme de prépa, connaître la théorie des distributions et avoir des notions en statistiques/théorie des probas, variables aléatoires et autres joyeusetés 🙂
C'est à dire, savoir calculer une espérance et une variance, savoir ce qu'est une variable aléatoire, une loi normale, un bruit, un processus stochastique, etc.
Le point de départ pour "démontrer" Kalman, c'est déjà de partir de l'estimateur optimal (moindre carrés) et de comprendre comment ça marche (mathématiquement parlant). (En calculant l'espérance, puis la variance (dont la limite converge vers Cramer-Rao))
Bon courage,
Ferdinand Piette
Merci pour votre réponse :smile:.
Bonjour comme la derniere personne ayant laissée un commentaire je suis etudiant en classe preparatoire en deuxieme année? Tout d'abord merci pour votre travail qui m'aide dans mes recherches.
J'ai un projet de fin d'annee qui pour ma part sera sur les batteries li-ion (lithium ion) mon but est de faire different type de decharge de batterie pour voir quel est le type d'utilisation qui deteriore le plus la batterie . Seulement pour cela j'ai besoin de connaitre le pourcentage de charge de la batterie, et normalement ca peut se faire par utilisation du filtre de kalman connaissez vous cette methode, avez vous deja utiliser un filtre de kalman pour cela ou avez vous des sources pouvant m'eclairer sur le filtre de kalman pour cette utilisation ??
Merci d'avance pour votre reponse
Alan
Bonjour,
Je ne vois pas en quoi le filtre de Kalman apportera quelque-chose dans ce cas. Il suffit de mesurer la tension aux bornes de l'accumulateur. Sachant que la Li-ion est déchargé à 2.5V et chargé à 4.2V, on peut facilement calculer le pourcentage de charge.
Pour affiner un peu le modèle, comme l'évolution de la tension n'est pas linéaire, on peut tracer la courbe de la décharge au cours du temps en branchant à l'accu une charge qui tire un courant constant.
Même si la mesure est très bruité (ce qui m'étonnerai beaucoup), prendre 5 mesures en peu de temps et les moyenner sera aussi efficace que d'appliquer un filtre de Kalman !
bonjour merci de votre reponse tres tres rapide
en effet pour quelques mesures comme ca ca pourrait le faire et encore vu comme la courbe de tension n'est pas du tout lineaire je ne sais pas ... mais surtout pour ma pars le but serait de faire une mesure précise durant toute la durée de vie d'une batterie avec différents type d'utilisation et en pouvant constater l'evolution de la capacite de la batterie au cour du temps et comme a la fin de la charge la tension ne varie que tres faiblement je ne pourrais faire quelque chose de precis ... enfin je pense ?!
je n'arrive meme pas a trouver de quoi est constitue le filtre de kalman ou si il peut s'acheter avec tous les composants relies je ne me rends pas compte de la technologie intrinseque a ce filtre ...
en fait, la tension aux bornes de l'accumulateur ne dépend pas que de l'état de charge de la cellule mais également de la tension aux bornes de la partie capacitive de l'impédance interne à la cellule.
d'où l'intérêt de l'utilisation d'un filtre de Kalman 🙂
salut vraiment les explication sur le filtre de kalman sont trop clair mais comment onpeut l'appliquer sur la machine asynchrone
bonne journée
bonsoir ,
est il possible d'avoir une aide sur la simulation de filtre de kalman sous matlab.
merci
Merci bcp pour ces explications!
j'ai un peu galéré au début de l'article parce que je ne comprenais pas pourquoi estimer la matrice de covariance était en général simple. Peut-être que l'explication à la fin de l'article pourrait-elle être mentionnée (même brièvement) plus haut?
Bonjour, je suis très débutant dans ce domaine,
Comment on peut calculer la matrice B, la vecteur du bruit de mesure (bruit gaussien engendré par les capteurs) ?
Merci
Merci
Bonsoir
Merci pour l'aide que vous nous apporter en partageant vos travaux.
je fais mon mémoire sur l'estimation des parametres dans un modèle déterminse épidémiologique en utilisant les observateurs adaptatifs.
Savez vous si c'est toujours possible de faire la reconstructions d'états et l'estimations des paramètres inconnues à l'aide des observateurs à entrée inconnue.
Merci d'avance
Merci pour ce tutoriel Mr FP
J'ai mis quelques jours pour faire tourner l'algorithme et ce pour l'application suivante:
Estimation du vecteur de symboles 4QAM dans une chaine de transmission numérique simple ( mono porteuse, canal plat invariant dans le temps) .
l’algorithme tourne bien (?) mais ma question est :
un vecteur de symboles M-QAM, sachant qu'il est variant dans le temps, est -il considéré comme :
* évoluant selon un processus linéaire aléatoire?
* évoluant selon un processus linéaire déterministe supposé connu?
ceci me permettrait de confirmer les résultats obtenus.
Je remercie celui ou celle qui pourrait m'orienter.
Bonjour,
M-QAM est le vecteur à estimer ?
Il faut dans ce cas modéliser l'évolution de ce vecteur de manière linéaire (même si la modélisation n'est pas parfaite).
Du coup, je dirais qu'il faut que les paramètres à estimer évoluent selon un processus linéaire déterministe.
merci bcp Mr FP
Bjr!
j aimerais avoir des explication svp sur comment estimer les parametres dun machine asynchrone par le filtre de kalman etendu?
thank you in advance!
bjr
moi aussi j'ai le même problème j aimerais avoir des explication svp sur comment estimer les parametres dun machine asynchrone par le filtre de kalman etendu?
bonjour,
je vous remercie pour cet article,
j' ai un projet porté sur la reconstruction de la trajectoire d'une moto en utilisant par filtre de KALMAN étendu sous MatLab .S'il vous plait vous n'auriez pas déjà réalisé un travail du genre par ce que je suis un peux en retard.
Au plaisir de vous lire
Bonjour,
d'après ce que j'ai cherché sur internet sur la méthode des moindre carrés, je ne la trouve utilisée que pour la régression linéaire(y=a*x+b),où on estime'' y'' par l'estimation de la pente de la droite '(a) et l'élément b.
je veux mettre une correspondance entre ce que est réalisé dans cet article et ce que j "ai trouvé comme exemple, mais je n'arrive pas à comprendre.
par ce que, dans cet article, je ne comprends pas que est ce que on doit estimer, est ce que c'est le X ou le H.
Ou c'est une autre application différente de celle de la régression linéaire.??,
SVP, je suis débutant j'en ai vraiment besoin, si quelqu'un a une réponse.
merci
bonjour
quelqu'un peut m'aider de me corrigé mon programme à propos l'observateur de filtre kalman étendu pour un système non linéaire machine synchrone à aiment permanent j'ai connus toute les entrées et meme les grandeurs non mesurable que je voulais estimer mais je n'arrive pas de corriger mon programme j'attends votre réponse
cordialement
Bonjour Ferdinand,
Tout d'abord je vous remercie pour le travail que vous avez fait. C'est vraiment très intéressant.
J'ai une question à vous poser svp: comment vous avez pu à écrire X_(k+1) en fonction de X_k?
Je vous remercie par avance.
Cordialement,
Bonjour et merci pour le tuto .. j aimerai estimer le Deplacement pedestre dans un batiment et le localisation d une personne indoor... avez vous une Idee comment modeliser un deplacemnt?
bonjour,
je vous remercie infiniment pour ces explications, c'est vraiment impeccable. je veux juste savoir pourquoi dans cet exemple "Les valeurs estimées par l'estimateur pourraient être les suivantes : 200, 260, 300, 220, 240, 160" nous avons 6 valeurs car j'ai pensé qu'un estimateur va nous donner une seule valeur estimée.